更通用、有效，蚂蚁自研优化器WSAM入选KDD Oral

机器之心专栏

机器之心编辑部

蚂蚁AIInfra团队在深度学习最核心之一的优化器方向持续投入与创新，实现了AI训练节约资源、加速收敛、提升泛化等目标。我们将推出“优化器三部曲”系列，这是本系列的第一篇。

深度神经网络（DNNs）的泛化能力与极值点的平坦程度密切相关，因此出现了Sharpness-AwareMinimization(SAM)算法来寻找更平坦的极值点以提高泛化能力。本文重新审视SAM的损失函数，提出了一种更通用、有效的方法WSAM，通过将平坦程度作为正则化项来改善训练极值点的平坦度。通过在各种公开数据集上的实验表明，与原始优化器、SAM及其变体相比，WSAM在绝大多数情形都实现了更好的泛化性能。WSAM在蚂蚁内部数字支付、数字金融等多个场景也被普遍采用并取得了显著效果。该文被KDD'23接收为OralPaper。

论文地址：

代码地址：

最近的研究表明，泛化能力与极值点的平坦程度密切相关，即损失函数“地貌”中平坦的极值点可以实现更小的泛化误差。Sharpness-AwareMinimization(SAM)[1]是一种用于寻找更平坦极值点的技术，是当前最有前途的技术方向之一。它广泛应用于各个领域，如CV、NLP和bi-levellearning，并在这些领域明显优于原先最先进的方法。

为了探索更平坦的最小值，SAM定义损失函数L在w处的平坦程度如下：

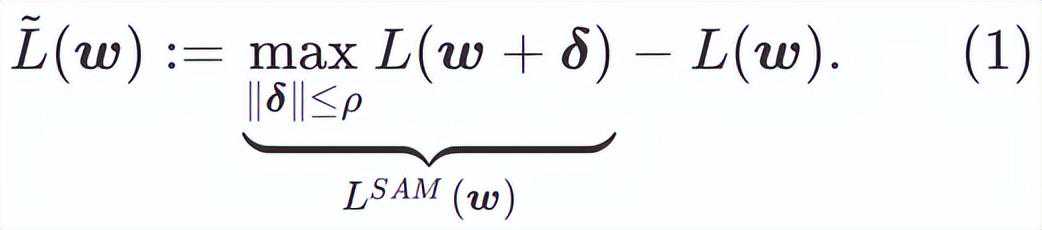
GSAM[2]证明了是局部极值点Hessian矩阵最大特征值的近似，表明确实是平坦（陡峭）程度的有效度量。然而只能用于寻找更平坦的区域而不是最小值点，这可能导致损失函数收敛到损失值依然很大的点（虽然周围区域很平坦）。因此，SAM采用，即作为损失函数。它可以视为在和之间寻找更平坦的表面和更小损失值的折衷方案，在这里两者被赋予了同等的权重。

本文重新思考了的构建，将视为正则化项。我们开发了一个更通用、有效的算法，称为WSAM（WeightedSharpness-AwareMinimization），其损失函数加入了一个加权平坦度项作为正则项，其中超参数控制了平坦度的权重。在方法介绍章节，我们演示了如何通过来指导损失函数找到更平坦或更小的极值点。我们的关键贡献可以总结如下。

我们提出WSAM，将平坦度视为正则化项，并在不同任务之间给予不同的权重。我们提出一个“权重解耦”技术来处理更新公式中的正则化项，旨在精确反映当前步骤的平坦度。当基础优化器不是SGD时，如SGDM和Adam，WSAM在形式上与SAM有显著差异。消融实验表明，这种技术在大多数情况下可以提升效果。

我们在公开数据集上验证了WSAM在常见任务中的有效性。实验结果表明，与SAM及其变体相比，WSAM在绝大多数情形都有着更好的泛化性能。

预备知识

SAM是解决由公式（1）定义的的极小极大最优化问题的一种技术。

首先，SAM使用围绕w的一阶泰勒展开来近似内层的最大化问题，即、

其次，SAM通过采用的近似梯度来更新w，即

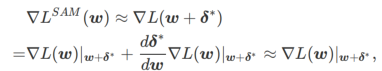
其中第二个近似是为了加速计算。其他基于梯度的优化器（称为基础优化器）可以纳入SAM的通用框架中，具体见Algorithm1。通过改变Algorithm1中的和，我们可以获得不同的基础优化器，例如SGD、SGDM和Adam，参见。请注意，当基础优化器为SGD时，Algorithm1回退到SAM论文[1]中的原始SAM。

方法介绍

WSAM的设计细节

在此，我们给出的正式定义，它由一个常规损失和一个平坦度项组成。由公式（1），我们有

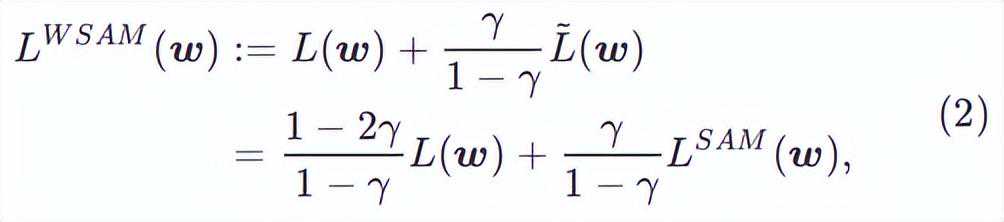
其中。当=0时，退化为常规损失；当=1/2时，等价于；当1/2时，更注重平坦度，因此与SAM相比更容易找到具有较小曲率而非较小损失值的点；反之亦然。

包含不同基础优化器的WSAM的通用框架可以通过选择不同的和来实现，见Algorithm2。例如，当和时，我们得到基础优化器为SGD的WSAM，见Algorithm3。在此，我们采用了一种“权重解耦”技术，即平坦度项不是与基础优化器集成用于计算梯度和更新权重，而是独立计算（Algorithm2第7行的最后一项）。这样，正则化的效果只反映了当前步骤的平坦度，而没有额外的信息。为了进行比较，Algorithm4给出了没有“权重解耦”（称为Coupled-WSAM）的WSAM。例如，如果基础优化器是SGDM，则Coupled-WSAM的正则化项是平坦度的指数移动平均值。如实验章节所示，“权重解耦”可以在大多数情况下改善泛化表现。

展示了不同取值下的WSAM更新过程。当1/2时，介于和之间，并随着增大逐渐偏离。

简单示例

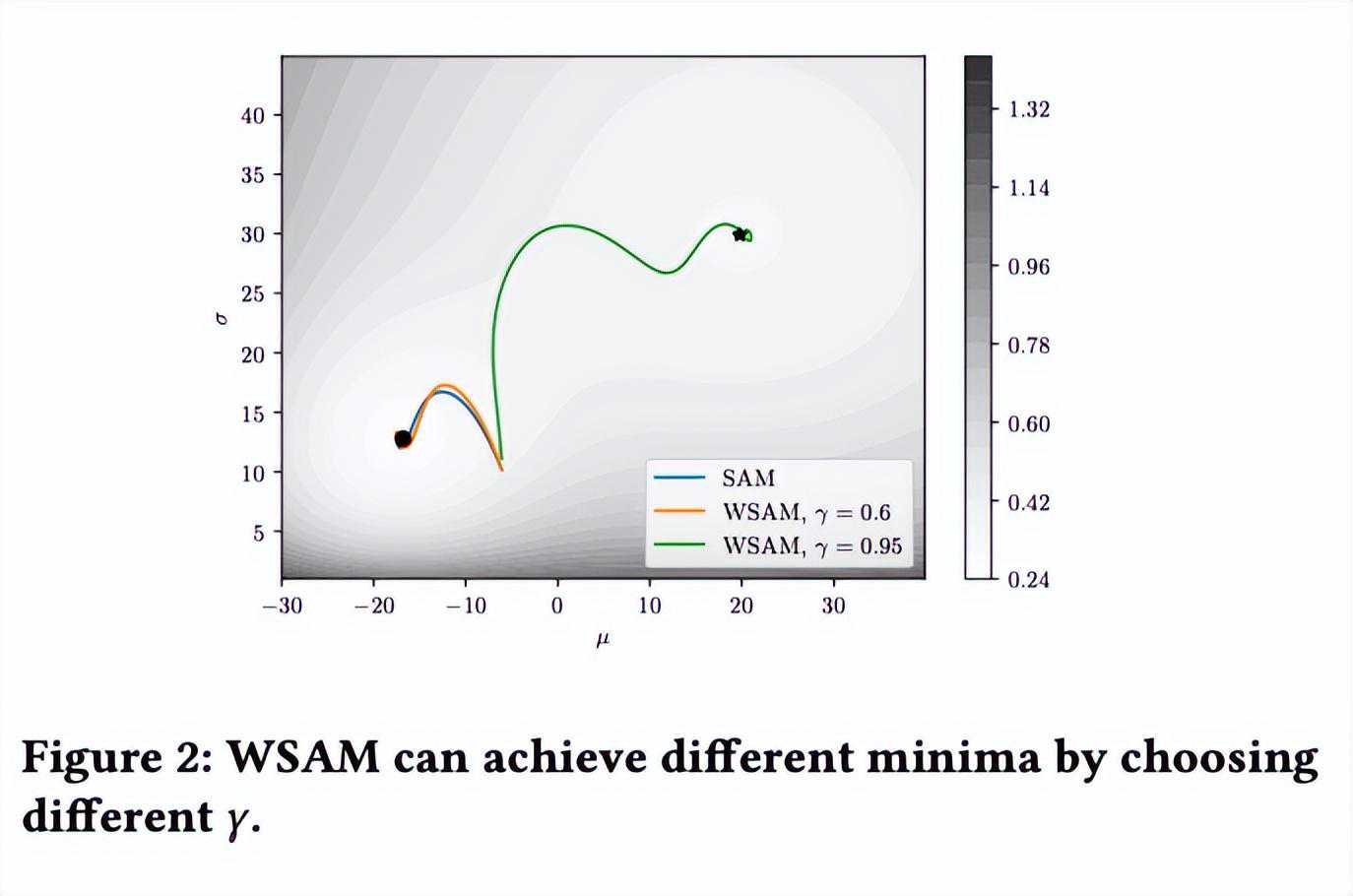
为了更好地说明WSAM中γ的效果和优势，我们设置了一个二维简单示例。如所示，损失函数在左下角有一个相对不平坦的极值点（位置：(-16.8,12.8)，损失值：0.28），在右上角有一个平坦的极值点（位置：(19.8,29.9)，损失值：0.36）。损失函数定义为:

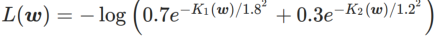
，这里

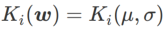
是单变量高斯模型与两个正态分布之间的KL散度，即

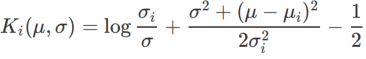
，其中

和

。

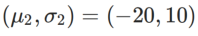
我们使用动量为0.9的SGDM作为基础优化器，并对SAM和WSAM设置=2。从初始点(-6,10)开始，使用学习率为5在150步内优化损失函数。SAM收敛到损失值更低但更不平坦的极值点，=0.6的WSAM也类似。然而，=0.95使得损失函数收敛到平坦的极值点，说明更强的平坦度正则化发挥了作用。

实验

我们在各种任务上进行了实验，以验证WSAM的有效性。

图像分类

我们首先研究了WSAM在Cifar10和Cifar100数据集上从零开始训练模型的效果。我们选择的模型包括ResNet18和WideResNet-28-10。我们使用预定义的批大小在Cifar10和Cifar100上训练模型，ResNet18和WideResNet-28-10分别为128，256。这里使用的基础优化器是动量为0.9的SGDM。按照SAM[1]的设置，每个基础优化器跑的epoch数是SAM类优化器的两倍。我们对两种模型都进行了400个epoch的训练（SAM类优化器为200个epoch），并使用cosinescheduler来衰减学习率。这里我们没有使用其他高级数据增强方法，例如cutout和AutoAugment。

对于两种模型，我们使用联合网格搜索确定基础优化器的学习率和权重衰减系数，并将它们保持不变用于接下来的SAM类优化器实验。学习率和权重衰减系数的搜索范围分别为{0.05,0.1}和{1e-4,5e-4,1e-3}。由于所有SAM类优化器都有一个超参数(邻域大小)，我们接下来在SAM优化器上搜索最佳的并将相同的值用于其他SAM类优化器。的搜索范围为{0.01,0.02,0.05,0.1,0.2,0.5}。最后，我们对其他SAM类优化器各自独有的超参进行搜索，搜索范围来自各自原始文章的推荐范围。对于GSAM[2]，我们在{0.01,0.02,0.03,0.1,0.2,0.3}范围内搜索。对于ESAM[3]，我们在{0.4,0.5,0.6}范围内搜索，在{0.4,0.5,0.6}范围内搜索，在{0.4,0.5,0.6}范围内搜索。对于WSAM，我们在{0.5,0.6,0.7,0.8,0.82,0.84,0.86,0.88,0.9,0.92,0.94,0.96}范围内搜索。我们使用不同的随机种子重复实验5次，计算了平均误差和标准差。我们在单卡NVIDIAA100GPU上进行实验。每个模型的优化器超参总结在中。

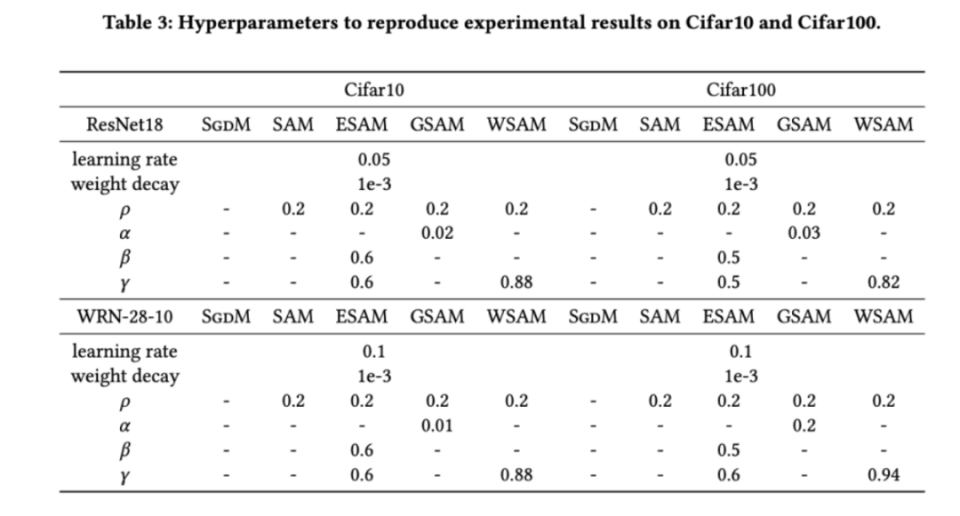
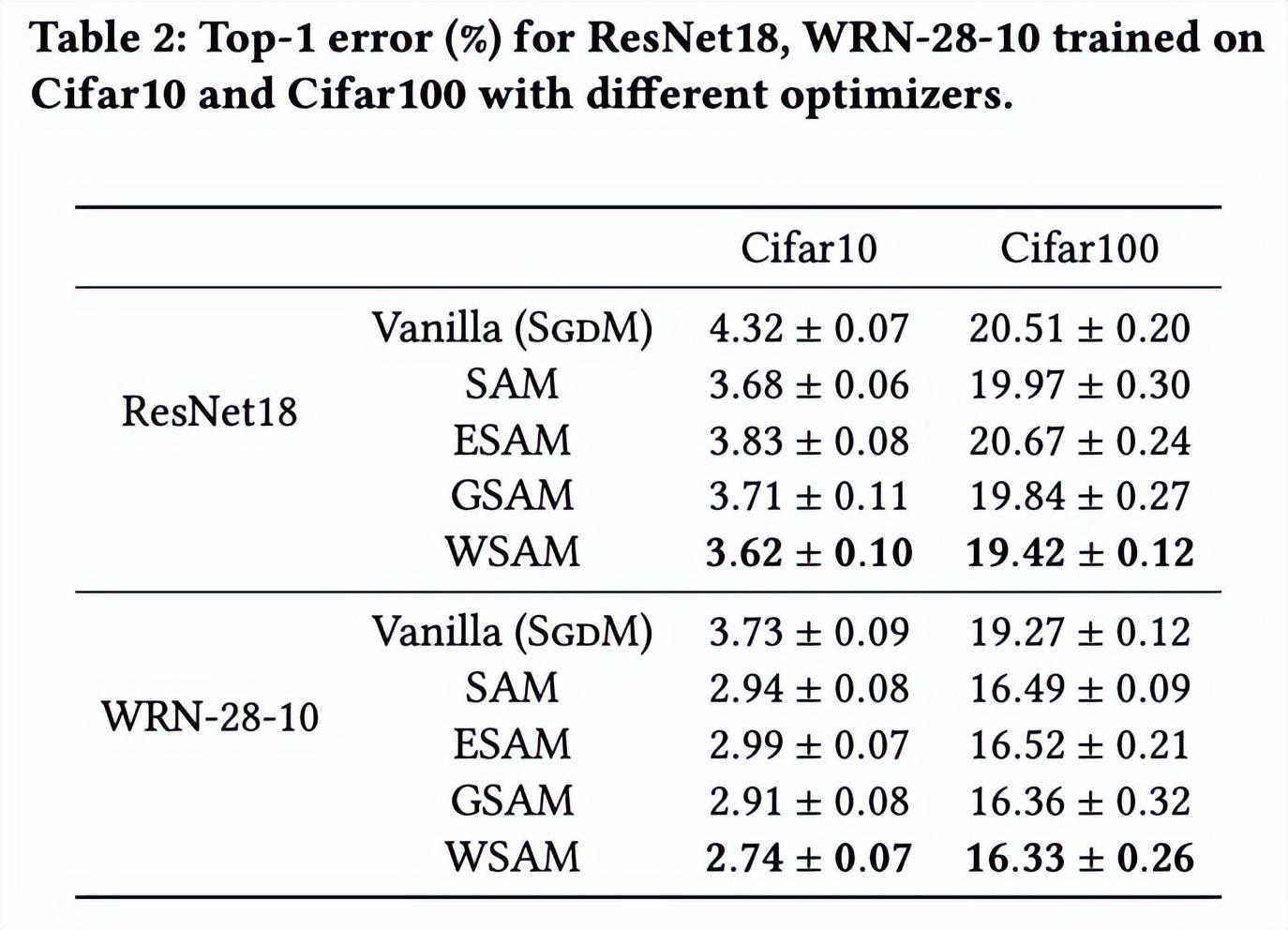
给出了在不同优化器下，ResNet18、WRN-28-10在Cifar10和Cifar100上测试集的top-1错误率。相比基础优化器，SAM类优化器显著提升了效果，同时，WSAM又显著优于其他SAM类优化器。

ImageNet上的额外训练

我们进一步在ImageNet数据集上使用Data-EfficientImageTransformers网络结构进行实验。我们恢复了一个预训练的DeiT-basecheckpoint，然后继续训练三个epoch。模型使用批大小256进行训练，基础优化器为动量0.9的SGDM，权重衰减系数为1e-4，学习率为1e-5。我们在四卡NVIDIAA100GPU重复跑5次并计算平均误差和标准差。

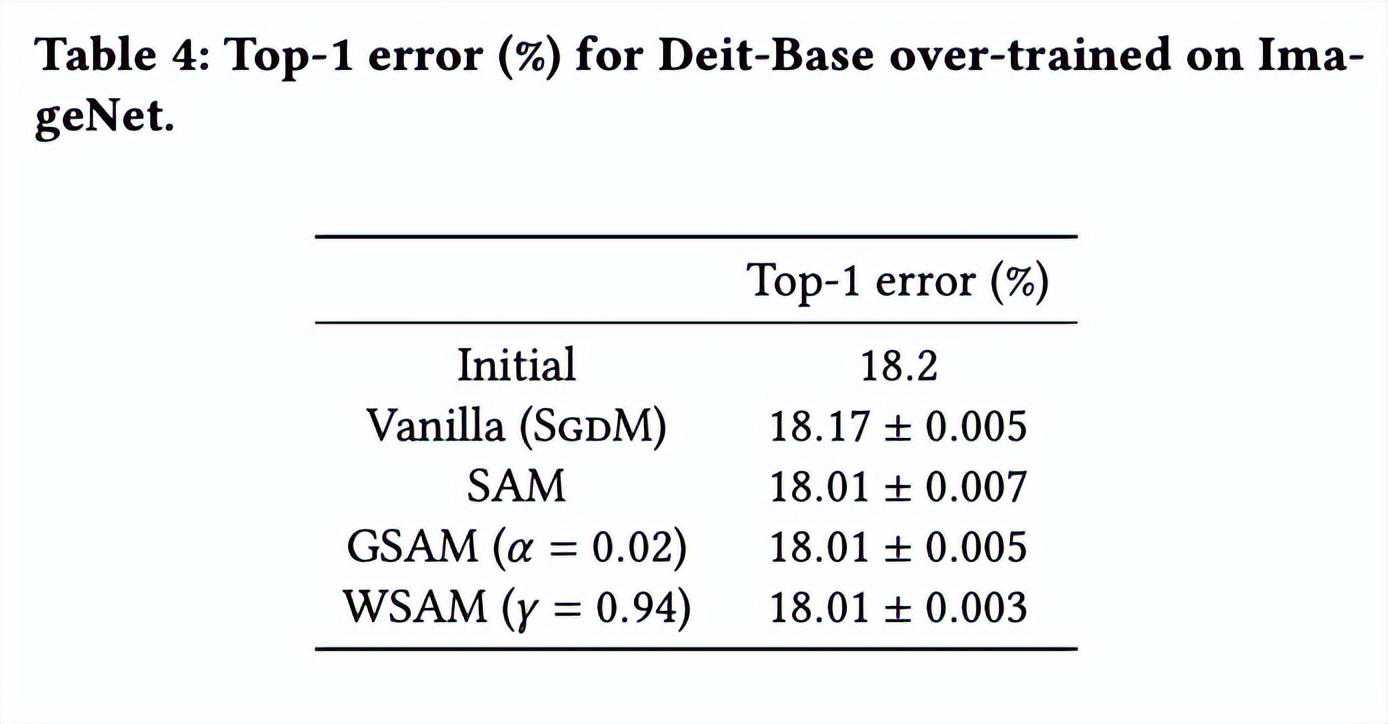
我们在{0.05,0.1,0.5,1.0,⋯,6.0}中搜索SAM的最佳。最佳的=5.5被直接用于其他SAM类优化器。之后，我们在{0.01,0.02,0.03,0.1,0.2,0.3}中搜索GSAM的最佳，并在0.80到0.98之间以0.02的步长搜索WSAM的最佳。

模型的初始top-1错误率为18.2%，在进行了三个额外的epoch之后，错误率如所示。我们没有发现三个SAM-like优化器之间有明显的差异，但它们都优于基础优化器，表明它们可以找到更平坦的极值点并具有更好的泛化能力。

标签噪声的鲁棒性

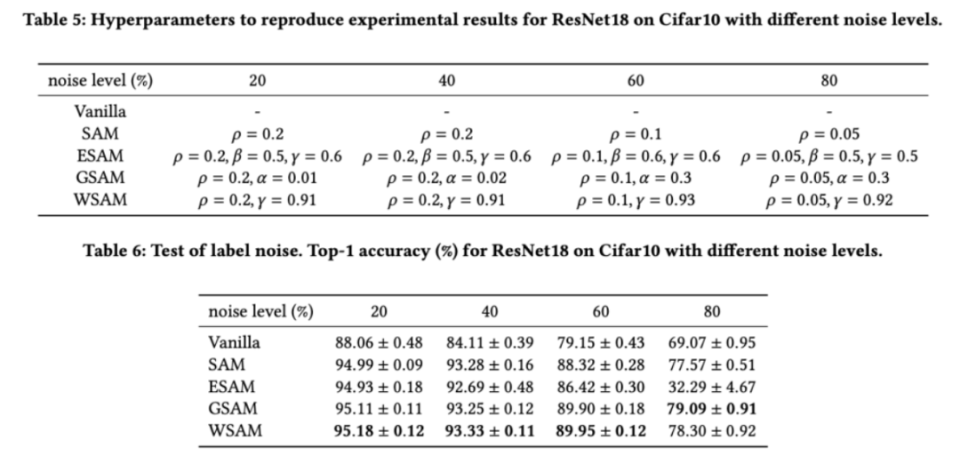
如先前的研究[1,4,5]所示，SAM类优化器在训练集存在标签噪声时表现出良好的鲁棒性。在这里，我们将WSAM的鲁棒性与SAM、ESAM和GSAM进行了比较。我们在Cifar10数据集上训练ResNet18200个epoch，并注入对称标签噪声，噪声水平为20%、40%、60%和80%。我们使用具有0.9动量的SGDM作为基础优化器，批大小为128，学习率为0.05，权重衰减系数为1e-3，并使用cosinescheduler衰减学习率。针对每个标签噪声水平，我们在{0.01,0.02,0.05,0.1,0.2,0.5}范围内对SAM进行网格搜索，确定通用的值。然后，我们单独搜索其他优化器特定的超参数，以找到最优泛化性能。我们在中列出了复现我们结果所需的超参数。我们在中给出了鲁棒性测试的结果，WSAM通常比SAM、ESAM和GSAM都具有更好的鲁棒性。

探索几何结构的影响

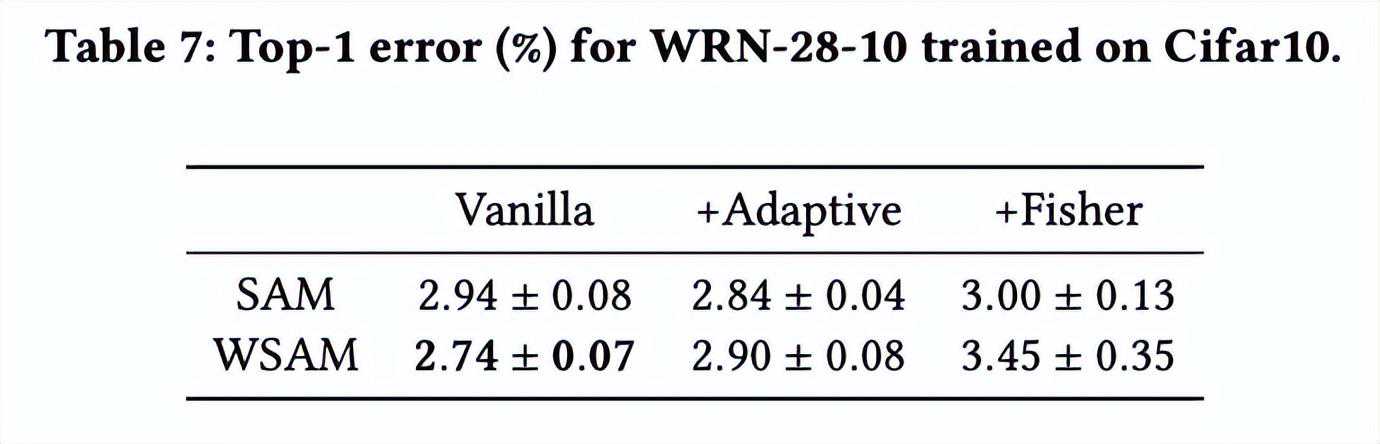
SAM类优化器可以与ASAM[4]和FisherSAM[5]等技术相结合，以自适应地调整探索邻域的形状。我们在Cifar10上对WRN-28-10进行实验，比较SAM和WSAM在分别使用自适应和Fisher信息方法时的表现，以了解探索区域的几何结构如何影响SAM类优化器的泛化性能。

除了和之外的参数，我们复用了图像分类中的配置。根据先前的研究[4,5]，ASAM和FisherSAM的通常较大。我们在{0.1,0.5,1.0,…,6.0}中搜索最佳的，ASAM和FisherSAM最佳的均为5.0。之后，我们在0.80到0.94之间以0.02的步长搜索WSAM的最佳，两种方法最佳均为0.88。

令人惊讶的是，如所示，即使在多个候选项中，基准的WSAM也表现出更好的泛化性。因此，我们建议直接使用具有固定的基准WSAM即可。

消融实验

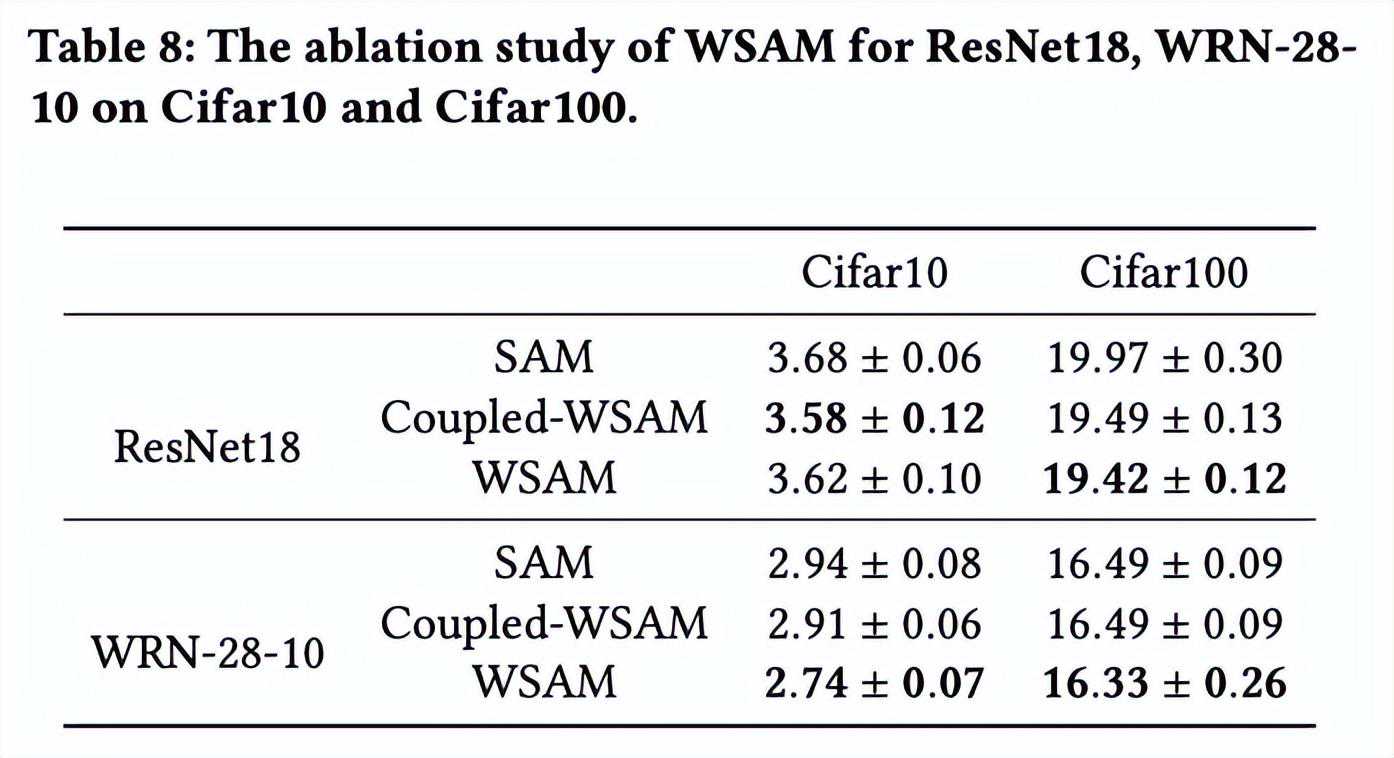
在本节中，我们进行消融实验，以深入理解WSAM中“权重解耦”技术的重要性。如WSAM的设计细节所述，我们将不带“权重解耦”的WSAM变体（算法4）Coupled-WSAM与原始方法进行比较。

结果如所示。Coupled-WSAM在大多数情况下比SAM产生更好的结果，WSAM在大多数情况下进一步提升了效果，证明“权重解耦”技术的有效性。

极值点分析

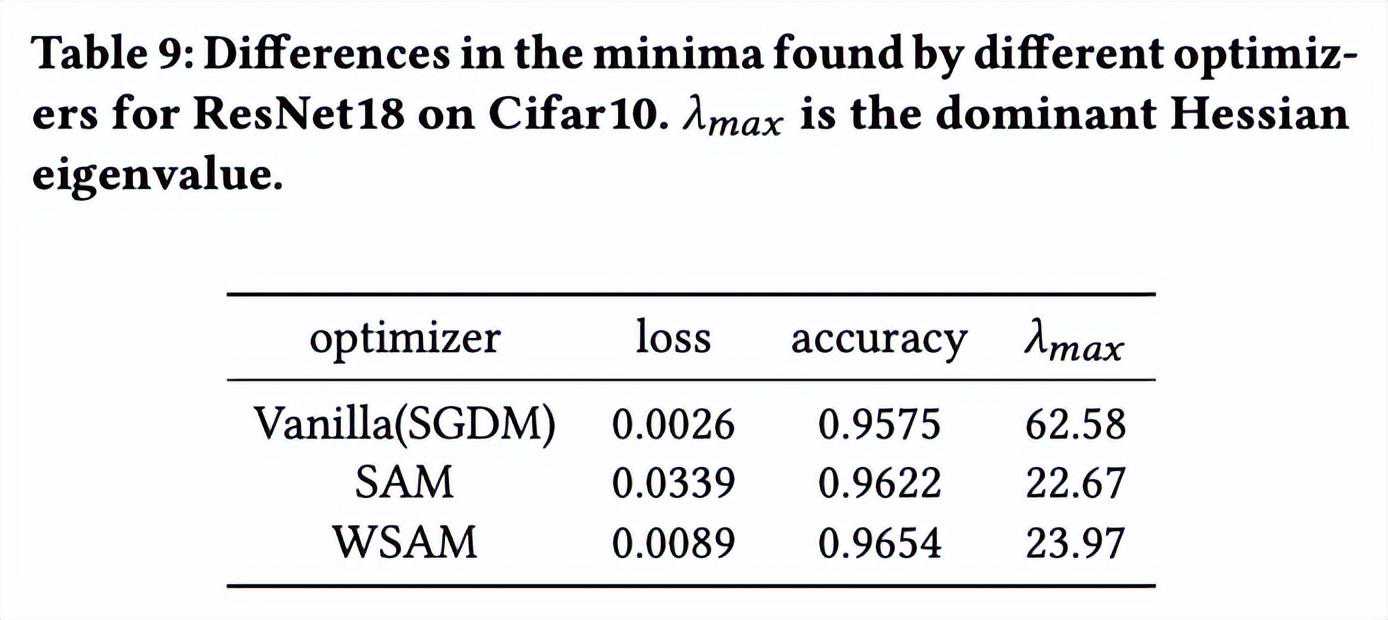
在这里，我们通过比较WSAM和SAM优化器找到的极值点之间的差异，进一步加深对WSAM优化器的理解。极值点处的平坦（陡峭）度可通过Hessian矩阵的最大特征值来描述。特征值越大，越不平坦。我们使用PowerIteration算法来计算这个最大特征值。

显示了SAM和WSAM优化器找到的极值点之间的差异。我们发现，vanilla优化器找到的极值点具有更小的损失值但更不平坦，而SAM找到的极值点具有更大的损失值但更平坦，从而改善了泛化性能。有趣的是，WSAM找到的极值点不仅损失值比SAM小得多，而且平坦度十分接近SAM。这表明，在寻找极值点的过程中，WSAM优先确保更小的损失值，同时尽量搜寻到更平坦的区域。

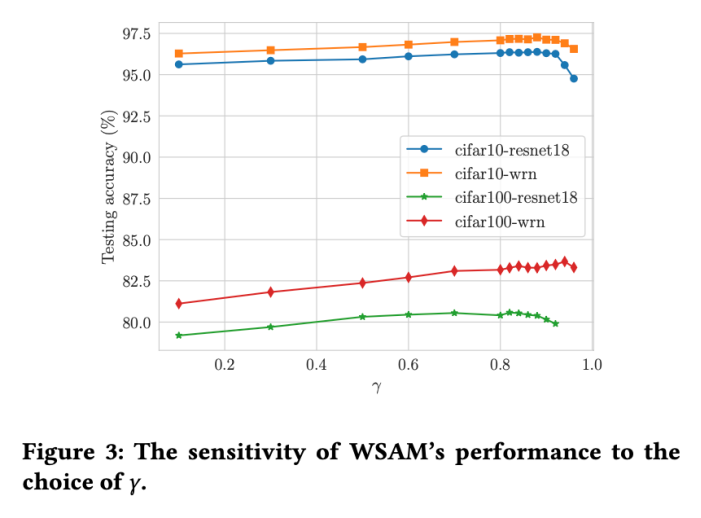
超参敏感性

与SAM相比，WSAM具有一个额外的超参数，用于缩放平坦（陡峭）度项的大小。在这里，我们测试WSAM的泛化性能对该超参的敏感性。我们在Cifar10和Cifar100上使用WSAM对ResNet18和WRN-28-10模型进行了训练，使用了广泛的取值。如所示，结果表明WSAM对超参的选择不敏感。我们还发现，WSAM的最优泛化性能几乎总是在0.8到0.95之间。

参考文献

[1]'21.

[2]'22.

[3]'22.

[4]:AdaptiveSharpness-'21.

[5]:'22.