面向可再生能源集成的综合能源系统熵态计算模型
- 技术分享
- 2024-11-10 11:16:57
- 13

面向可再生能源集成的综合能源系统熵态计算模型李宜哲1✉王丹1,2✉李家熙1✉贾宏杰1,2周天烁1刘佳委11.智能电网教育部重点实验室(天津大学),天津市300072;2.天津市智慧能源与信息技术重点实......
李宜哲1✉
王丹1,2✉
李家熙1✉
贾宏杰1,2
周天烁1
刘佳委1
1.智能电网教育部重点实验室(天津大学),天津市300072;2.天津市智慧能源与信息技术重点实验室(天津大学),天津市300072
最近更新:2024-03-26
DOI:10.7500/AEPS20230813002
摘要综合能源系统(IES)熵态机理与分析方法为面向可再生能源集成的IES能量品质分析提供了一种新的理论基础。针对不同的能源系统规模和场景,如何系统性求解大规模能源系统熵态分布是后续系统规划、运行和能量管控等亟须解决的基础问题之一。在IES熵态理论的基础上,进一步梳理了系统熵态分布的计算体系与思路;根据熵增流求解的需要,定义了一些关键计算矩阵与计算列向量;结合IES㶲流模型和熵态网络的定义,考虑能量枢纽(能源站)熵增流转化与分配机制,建立了基于顺序求解和联立求解的IES熵态计算模型,通过算例验证了两种计算模型的正确性与有效性,并讨论了两种计算方法的异同与适用性。
关键词综合能源系统;可再生能源;能量品质;熵态;熵增流;㶲流;㶲损
0引言IES㶲流模型针对各类能量传输介质所含的有效能,将能量流中的有效部分视为IES㶲流,定义能量传输和转化环节的有效能损失为IES㶲损,构建网络化模型以研究㶲流在系统中的分布情况。
IES熵态机理模型对系统供能过程产生的能量不可用性进行量化分析,并寻求有利于量质协同发展目标的IES规划与运行决策[8-9]。能量生产、转化、传输会导致能量的退化,再生能源和负荷的不确定性导致能量无序程度增加。上述因素加剧了能量的不可用性,即IES熵增。熵态机理模型以熵增源表示产生熵增的环节,以熵增流量化不可用性层面的能量品质,通过熵态网络描述熵增流在系统中分布与流动,并指明熵增流在熵态网络中的传播机理与规则。针对不同的能源系统规模和场景,如何进行快速、准确的IES熵态计算是一个基础性的关键问题。
IES是由多个子系统组成的复杂网络结构[10-11],考虑能源系统网络属性对于理解能量在系统中的分布、传播和转化过程具有重要意义[8,12]。矩阵化计算方法能够将网络建模和分析问题转化为矩阵变换和线性代数问题[13-14],降低运算的复杂性并提升求解效率。
本文基于IES熵态机理模型的网络属性,构建矩阵化熵态方程组,实现熵态计算从递推运算向线性方程求解的转变,进而提出基于顺序和联立求解的IES熵态计算模型,讨论了两种模型的适用性并通过算例验证其有效性。
1熵态网络的熵态方程1.1方程构建思路IES熵态机理模型定义了IES熵增,反映能量生产、传输、转化等过程以及可再生能源不确定性导致的无序性增量,包括传统热力学熵增和信息学等效热力学熵增。考虑能源系统的网络化特征,定义熵增流为㶲流传播路径上的熵增叠加量,作为㶲流的品质标签,以熵态网络描述系统内熵增流的传播和分布情况[7],熵态网络由节点、支路以及熵增源构成。支路和节点是描述网络输送与分配环节的熵态元件,熵态网络的拓扑结构取决于节点与支路的连接关系。熵增源描述能量环节的熵增属性,在熵态网络中对熵增流产生增量的作用,即熵增源流出与流入的熵增流之差为对应系统环节产生熵增。上述能量环节可以是产生能量/有效能损耗的管线支路、能量转化设备,以及含有不确定性的可再生能源设备等。节点表征能量传输过程中的聚合与分配环节,能量介质在此处混合均匀,流出时具有同等能量品质属性。因此,节点流出熵增流比例与介质比例一致,且与㶲流的比例一致。
综上所述,熵增流经过各组成元件时遵循IES熵态机理的约束,其中,描述网络属性的约束包括IES节点熵态平衡关系和节点熵态分配关系[7]。二者是构建方程组的关键,具体而言:1)IES节点熵态平衡关系反映流入节点的总熵增流与节点熵增的恒等关系;2)IES节点熵态分配关系反映流出节点的熵增流与节点熵增的比例关系,该比例关系遵从㶲流分配比例关系。熵态网络组成元件、元件参数以及建模机理的关系如图1所示。

图1熵态网络元件、参数和建模机理关系
,parameters,andmodelingmechanismofentropystatenetwork
为了快速、准确地计算熵态网络的熵增流分布情况,本文基于上述熵态关系和已达稳态平衡的㶲流分布[15],提出了节点熵态平衡方程与节点熵态分配方程(简称熵态方程),通过求解熵态方程可得熵态网络的熵态分布。
根据熵态方程的求解需要,提出以下关键的熵态方程参数列向量与关联矩阵,为计算方法奠定基础。已知某系统具有N个节点、M个支路,其中,K个节点存在多能负荷,P个节点存在电、气、热源,且已知网络拓扑结构和稳态㶲流分布[15]。
1.2方程组成元素:节点-支路关联矩阵节点-支路关联矩阵为N×M�×�矩阵,表示为A=(Ai,j)N×M�=(��,�)�×�。熵增流为㶲流的品质标签,二者传播方向一致,利用㶲流计算模型[8]可求解系统稳态㶲流分布,进而确定熵增流的传播方向。定义该矩阵的目的是为了描述系统结构,在熵态网络拓扑结构层面给定熵增流分布的边界条件,为构建熵态方程奠定基础。该矩阵既包含系统节点与支路连接关系,又包含系统稳态支路的方向信息。矩阵A�中的元素Ai,j��,�具体定义如下:若节点i(i=1,2,⋯,N�=1,2,⋯,�)与支路j(j=1,2,⋯,M�=1,2,⋯,�)相连,且㶲流由支路j流向节点i,则Ai,j=1��,�=1;若由节点i流向支路j,则Ai,j=−1��,�=-1;其他情况下Ai,j=0��,�=0。
将A�中−1-1元素置0,得到流入节点-支路关联矩阵A+�+,反映各节点与流入该节点的支路之间的连接关系,用于构建节点熵态平衡方程;将−A-�中−1-1元素置0,得到流出节点-支路关联矩阵A−�-,反映各支路与流出节点的连接关系,用于构建节点熵态分配方程。
1.3方程组成元素:㶲流参数列向量稳态平衡的㶲流分布是求解系统熵态分布的必要已知条件,用于确定各熵增源的熵增和各分配环节的熵增流比例。向量化熵态网络㶲流参数是描述㶲流分布、限定熵增流分布的边界条件以及构建矩阵形式熵态方程的关键因素。本文定义以下㶲流参数列向量,为构建熵态方程奠定基础。
支路㶲流为能量传输介质在支路首端所含有效能,支路㶲流的传播方向与介质相同。对于电力、天然气、热力系统而言,其㶲流分别对应有功功率、化学能释放的有效能、热水所含的有效能[15]。支路㶲损即为介质在支路上损失的有效能,即支路首末段的㶲流差值。
对于电力系统的某段支路,支路㶲流eb,ele�b,ele、支路㶲损ΔeeleΔ�ele可表示为:
eb,ele=P�b,ele=�
(1)
Δeele=PlossΔ�ele=�loss
(2)
式中:P�为电力支路有功功率;Ploss�loss为电力支路有功损耗。
对于天然气系统的某段支路,支路㶲流eb,gas�b,gas、支路㶲损ΔegasΔ�gas可表示为:
eb,gas=10003600(1−TaTgas−TalnTgasTa)Gmgas�b,gas=100036001-�a�gas-�aln�gas�a��gas
(3)
Δegas=0Δ�gas=0
(4)
式中:Tgas�gas为天然气的理论燃烧温度;Ta�a为环境温度;G�为天然气总热值;mgas�gas为天然气支路气流率。
对于热力系统的某段支路,支路㶲流eb,heat�b,heat、支路㶲损ΔeheatΔ�heat可表示为:
eb,heat=(T1−T1lnT1−Ta+TalnTa)cpmheat�b,heat=(�1-�1ln�1-�a+�aln�a)�p�heat
(5)
Δeheat=(T2−T1−T2lnT2+T1lnT1)cpmheatΔ�heat=(�2-�1-�2ln�2+�1ln�1)�p�heat
(6)
式中:T1�1和T2�2分别为热力支路首、末端的水温;cp�p为水的比热容;mheat�heat为热力支路水流率。
定义支路㶲流列向量为eb�b,维数为M�,设支路j的支路㶲流为eb,j�b,�,则eb�b可表示为:
eb=[eb,1eb,2⋯eb,M]T�b=[�b,1�b,2⋯�b,�]T
(7)
定义支路㶲损列向量为ΔeΔ�,维数为M�,设支路j的㶲损为ΔejΔ��,则ΔeΔ�可表示为:
Δe=[Δe1Δe2⋯ΔeM]TΔ�=[Δ�1Δ�2⋯Δ��]T
(8)
负荷㶲是由负荷消耗的㶲。电力系统的负荷㶲即为负荷有功功率;在天然气系统中可根据负荷气流量,采用与天然气支路㶲流相似的方法计算负荷㶲;在热力系统中即为流入与流出负荷的㶲流之差,如式(9)所示。
eL,heat=eLin,heat−eLout,heat�L,heat=�Lin,heat-�Lout,heat
(9)
式中:eL,heat�L,heat为热力负荷㶲;eLin,heat�Lin,heat为流入负荷的㶲流;eLout,heat�Lout,heat为流出负荷的㶲流。
定义负荷㶲流列向量为N维列向量,表示为eL=(eL,i)N×1�L=(�L,�)�×1,其中,元素eL,i�L,�的具体定义如下:若节点i为第k�(k=1,2,⋯,K�=1,2,⋯,�)个存在负荷的节点,且负荷㶲为ρk��,则eL,i=ρk�L,�=��;否则eL,i=0�L,�=0。
为便于在熵态方程中表达节点熵态分配关系,需要向量化节点流出㶲流和㶲流占比。定义以下㶲流辅助列向量作为方程的中间量。
定义节点流出总㶲流列向量为eoN�oN,维数为N,其中,各行元素对应各节点流出的㶲流总和,包括各节点流出支路㶲流与负荷㶲。采用A−�-描述支路与其首端节点的连接关系,从而构建eoN�oN如下:
eoN=A−eb+eL�oN=�-�b+�L
(10)
定义节点流出总㶲流倒数列向量为eoNi�oNi,维数为N,eoNi�oNi中各元素为eoN�oN中对应元素的倒数,其计算方法如式(11)所示。
eoNi=diag(eoN)−1ε=diag(A−eb+eL)−1ε�oNi=diag(�oN)-1�=diag(�-�b+�L)-1�
(11)
式中:ε�为元素均为1的N维列向量。
定义㶲流比例系数列向量为cpr�pr,为支路㶲流与其首端节点流出总㶲流的比值构成的列向量,维数为M。采用A−�-描述支路与其首端节点的对应关系,从而构建cpr�pr如下:
cpr=diag(eb)AT−eoNi=diag(eb)AT−diag(A−eb+eL)−1ε�pr=diag(�b)�-T�oNi=diag(�b)�-Tdiag(�-�b+�L)-1�
(12)
1.4方程组成元素:熵态参数列向量向量化的熵态参数是表达熵态关系的核心要素之一,本节将针对熵态方程中已知和待求熵态参数列向量进行定义,并讨论已知熵态参数的基本获取方法,为构建熵态方程奠定基础。
1.4.1已知熵态参数列向量
定义支路熵增源列向量为ΔShΔ�h,维数为M,其元素为各支路熵增源产生的传统热力学熵增,表征有效能损失带来的系统无序性增量。根据熵态机理模型[7],支路j熵增源产生的熵增ΔSh,jΔ�h,�可由支路㶲损ΔejΔ��计算,如式(13)所示,其向量形式ΔShΔ�h可由支路㶲损列向量ΔeΔ�计算,如式(14)所示。
ΔSh,j=ΔejTaΔ�h,�=Δ���a
(13)
ΔSh=1TaΔeΔ�h=1�aΔ�
(14)
信息熵能够量化不确定源荷能量的无序性,借助广义信息功的量化方法,可计算不确定性源荷能量导致的信息学等效热力学熵增[7]ΔSinfoΔ�info如下:
ΔSinfo=pinfofinfoTaΔ�info=�info�info�a
(15)
式中:pinfo�info和finfo�info分别为不确定性源荷能量的信息势和信息流,如式(16)和式(17)所示。
pinfo=Pmax−Pmins�info=�max-�min�
(16)
finfo=H=−∑is=1sPis(x)lnPis(x)�info=�=-∑��=1����(�)�����(�)
(17)
式中:Pmax�max和Pmin�min分别为不确定源荷能量的最大值和最小值;s�为划分微观状态的数量;H�为不确定性信息熵;Pis(x)��s(�)为归一化能量数据处于第is�s个状态的概率。
定义负荷信息熵增源列向量为N维列向量,表示为ΔSinfo=(ΔSinfo,i)N×1Δ�info=(Δ�info,�)�×1,其元素具体定义如下:若节点i为第k�个存在负荷的节点,且负荷产生的信息学等效热力学熵增为σk��,则ΔSinfo,i=σkΔ�info,�=��;否则ΔSinfo,i=0Δ�info,�=0。根据熵态机理模型[7],σk��的计算方法如下:
σk=pinfo,kfinfo,kTa��=�info,��info,��a
(18)
式中:pinfo,k�info,�为负荷k产生的信息势;finfo,k�info,�为负荷k产生的信息流。
节点注入熵增流为外部注入熵态网络的熵增流,来自其他熵态网络或可再生能源设备对应的熵增源,本文称之为源。定义节点注入熵增流列向量为N维列向量,表示为ΔSin=(ΔSin,i)N×1Δ�in=(Δ�in,�)�×1,其元素具体定义如下:若节点i为第p�(p=1,2,⋯,P�=1,2,⋯,�)个存在源的节点,且源注入节点的熵增流为ζp��,则ΔSin,i=ζpΔ�in,�=��;否则ΔSin,i=0Δ�in,�=0。
1.4.2待求熵态参数列向量
熵态计算的首要目标为计算网络熵态分布和负荷熵态分布,分别包含所有支路的支路熵增流和所有节点的节点熵增、负荷熵增,以及补充负荷节点熵增。支路熵增流为支路首端的熵增流;节点熵增为注入该节点的熵增流总和;负荷熵增为流出熵态网络并流向多能负荷或其他熵态网络的熵增流;补充负荷节点吸收负荷熵增和负荷信息熵增源注入的熵增流,表征各负荷节点对应的总熵增。
定义支路熵增流列向量为ΔSfΔ�f,维数为M,设支路j首端熵增流为ΔSf,jΔ�f,�,则ΔSfΔ�f可表示为:
ΔSf=[ΔSf,1ΔSf,2⋯ΔSf,M]TΔ�f=[Δ�f,1Δ�f,2⋯Δ�f,�]T
(19)
定义节点熵增列向量为ΔSNΔ�N,维数为N,设节点i的节点熵增为ΔSN,iΔ�N,�,则ΔSNΔ�N可表示为:
ΔSN=[ΔSN,1ΔSN,2⋯ΔSN,N]TΔ�N=[Δ�N,1Δ�N,2⋯Δ�N,�]T
(20)
定义负荷熵增列向量为N维列向量,表示为ΔSfL=(ΔSfL,i)N×1Δ�fL=(Δ�fL,�)�×1,其元素具体定义如下:若节点i为第k�个存在负荷的节点,且流向负荷的熵增流为φk��,则ΔSfL,i=φkΔ�fL,�=��;否则ΔSfL,i=0Δ�fL,�=0。
定义补充负荷节点熵增列向量为ΔSLΔ�L,维数为N。ΔSLΔ�L中各元素包含了各节点对应负荷的全部熵增,即节点流向负荷的熵增流和负荷不确定性导致的信息学等效热力学熵增。ΔSLΔ�L的计算公式如下:
ΔSL=ΔSfL+ΔSinfoΔ�L=Δ�fL+Δ�info
(21)
1.5子方程:节点熵态平衡方程根据IES熵态机理模型中定义的熵增源两端熵增流关系[7],支路末端熵增流为支路首端熵增流与支路熵增源之和。定义支路末端熵增流列向量为ΔSefΔ�fe,其计算公式如下:
ΔSef=ΔSf+ΔShΔ�fe=Δ�f+Δ�h
(22)
根据IES节点熵态平衡关系[7],采用A+�+描述支路与其末端节点的对应关系,构建ΔSNΔ�N如下:
ΔSN=ΔSin+A+ΔSefΔ�N=Δ�in+�+Δ�fe
(23)
将式(22)代入式(23),可得节点熵态平衡方程来表示ΔSNΔ�N、ΔSfΔ�f之间的恒等关系,如式(24)所示。
ΔSN=ΔSin+A+(ΔSf+ΔSh)Δ�N=Δ�in+�+(Δ�f+Δ�h)
(24)
1.6子方程:节点熵态分配方程由IES节点熵态分配关系可知:支路熵增流与首端节点熵增之比等于该支路㶲流与支路首端节点流出总㶲流之比,节点流向负荷的熵增流与节点熵增之比等于负荷㶲流与节点流出总㶲流之比。根据上述关系,采用A−�-描述支路与其首端节点的对应关系,借助中间量cpr�pr和eoNi�oNi构建节点熵态分配方程如下:
ΔSf=diag(cpr)AT−ΔSNΔ�f=diag(�pr)�-TΔ�N
(25)
ΔSfL=diag(ΔSN)diag(eL)eoNiΔ�fL=diag(Δ�N)diag(�L)�oNi
(26)
式(24)至式(26)提供了N+M+K个子方程,方程变量的总数为N+M+K,此时子方程总数与变量总数相等,满足求解方程组的要求。
1.7求解方法联立式(12)、式(24)和式(25)可得ΔSNΔ�N的计算公式如式(27)所示,其中,等号右边均为已知量。
ΔSN=(E−A+diag(diag(eb)AT−diag(A−eb+eL)−1ε)AT−)−1(ΔSin+A+ΔSh)Δ�N=(�-�+diag(diag(�b)�-Tdiag(�-�b+�L)-1�)�-T)-1(Δ�in+�+Δ�h)
(27)
式中:E�为N×N�×�单位矩阵。
得到ΔSNΔ�N后,联立式(12)和式(25)可得ΔSfΔ�f如下:
ΔSf=diag(diag(eb)AT−diag(A−eb+eL)−1ε)AT−ΔSNΔ�f=diag(diag(�b)�-Tdiag(�-�b+�L)-1�)�-TΔ�N
(28)
熵态网络的节点熵增与支路熵增流,即网络熵态分布均可计算。视ΔSNΔ�N为已知,根据式(26)可得ΔSfLΔ�fL,进而根据式(21)计算ΔSLΔ�L,得到负荷熵态分布。
熵态网络各参数、变量与熵态方程在求解过程中的关系如图2所示。
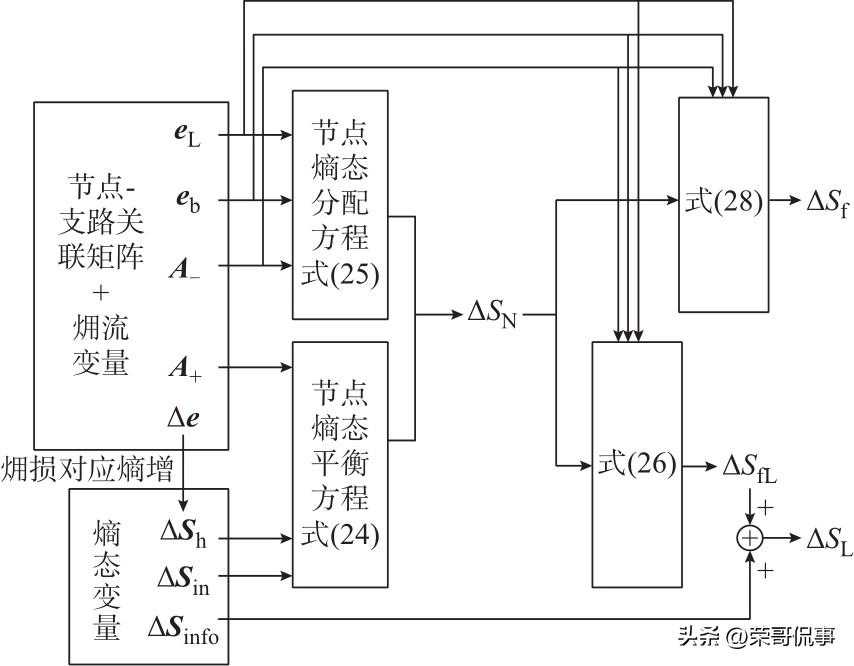
图2熵态网络参数、变量与方程的关系示意图
,variablesandequationsofentropystatenetwork
1.8熵态网络、方程、计算模型之间的关系IES熵态计算模型考虑能源系统各环节的熵增机理,以及能量转化环节对熵增流的分配机制,基于熵态方程求解系统的熵态分布。具体而言,根据耦合环节和多能管网的拓扑结构等熵态建模关键信息,确定IES熵态计算模型的熵态网络;根据能量生产设备、传输管线、多能负荷等熵增环节的熵态特征,确定IES熵态计算模型的熵态方程必要已知参数;求解熵态方程进而获取系统全局熵态分布。
能量枢纽(energyhub,EH)是进行多种能量相互转化的环节,相关设备产生传统热力学熵增和信息学等效热力学熵增[2,16]。本文将一定规模的EH称为能源站(energystation,ES)[17],其含有多种能量生产和转化设备,如热电联产(combinedheatandpower,CHP)、燃气锅炉(gasboiler,GB)、光伏(photovoltaic,PV)等,多种转化设备的协同互联使ES具有复杂的熵增流分配机制。本文针对ES提出两种建模思路:
1)将ES视为独立子系统,分别定义ES、电、气、热分立的熵态网络,依次求解各分系统熵态方程;
2)采用熵态节点和支路的形式表达ES熵态特征,以此连接其他系统的熵态网络,形成IES全系统熵态网络,直接求解全系统熵态方程。
针对ES熵态特性,基于上述两种ES熵态建模思路,本文提出了基于顺序求解的熵态计算模型和基于联立求解的熵态计算模型。
2基于顺序求解的熵态计算模型基于顺序求解的熵态计算模型针对电力、天然气、热力系统(简称为“能源子系统”)以及ES定义分立的熵态网络,以负荷熵增和节点注入熵增流的形式表达各分系统熵态网络之间交互的熵增流。因此,需要根据㶲流传播的方向顺序求解各分系统熵态方程,并将反映熵增流交互部分的结果作为已知量代入下一级熵态网络的熵态方程,直到完成全部分系统熵态计算。建立模型的关键在于确定各分系统的熵态网络拓扑结构,明确各分系统熵增环节的计算方法,为各分系统熵态方程提供必要已知参数。
2.1各分系统熵态网络结构定义2.1.1能源子系统熵态网络
电力、天然气系统的熵态网络拓扑结构与熵态机理模型一致,本文算例的IES如附录A图A1所示,其中,电力、天然气熵态网络结构如图A2和图A3所示。热力系统存在供回水双层对称网络结构,且热力热源和负荷处存在进水和出水端口,相比电力、天然气系统网络结构更为复杂。为了描述熵增流在热源和热负荷处的具体行径,须扩充㶲流模型拓扑结构以形成热力系统熵态网络。
将热力负荷出口节点视为热力系统熵态网络的一部分,定义负荷出口节点与供水网、回水网之间的支路为负荷进水支路、负荷出水支路,共称负荷支路。新增支路对应㶲流即为㶲流模型相应供回水节点的负荷㶲,负荷出口节点流向负荷的㶲流即相应负荷的负荷㶲损。
设某热力系统供水网节点数为nh,n�h,n,供水网支路数为nh,b�h,b,回水网节点数和支路数与供水网相同,热力负荷数为nh,L�h,L,则热力系统熵态网络的节点数为2nh,n+nh,L2�h,n+�h,L,支路数为2nh,b+2nh,L2�h,b+2�h,L。附录A图A4为算例IES的热力系统熵态网络示意图,该系统㶲流模型的网络拓扑结构为5节点10支路的双层对称供回水网络,熵态模型的网络拓扑结构为13节点16支路的单层网络。
2.1.2能量枢纽(能源站)熵态网络
ES熵态网络应能够反映上述两种熵增以及熵增流分配特性。ES熵态建模的研究目前仍处于初级阶段,有待进一步提高精细化程度。因此,ES熵态模型设置了独立的ES补充输入、输出节点,对ES内部网络结构不做约束,保留较为开放的ES熵增特性与ES熵增流分配机制,以采用多样化的ES熵态模型。本文采用下述ES熵态模型作为示例[18]。
设某ES存在ninES�ESin组输入熵增流、noutES�ESout组输出熵增流,与各电、气、热系统节点进行交互,各系统节点注入ES的熵增流经补充节点流向ES输入节点,经能源站支路以及等效熵增源ΔSESΔ�ES注入输出节点,然后经补充节点注入下级熵态网络。ES熵态计算模型的节点数为ninES�ESin+noutES�ESout+2、支路数为ninES�ESin+noutES�ESout+1,拓扑结构如图3所示。算例系统的ES熵态网络结构如附录A图A5所示。
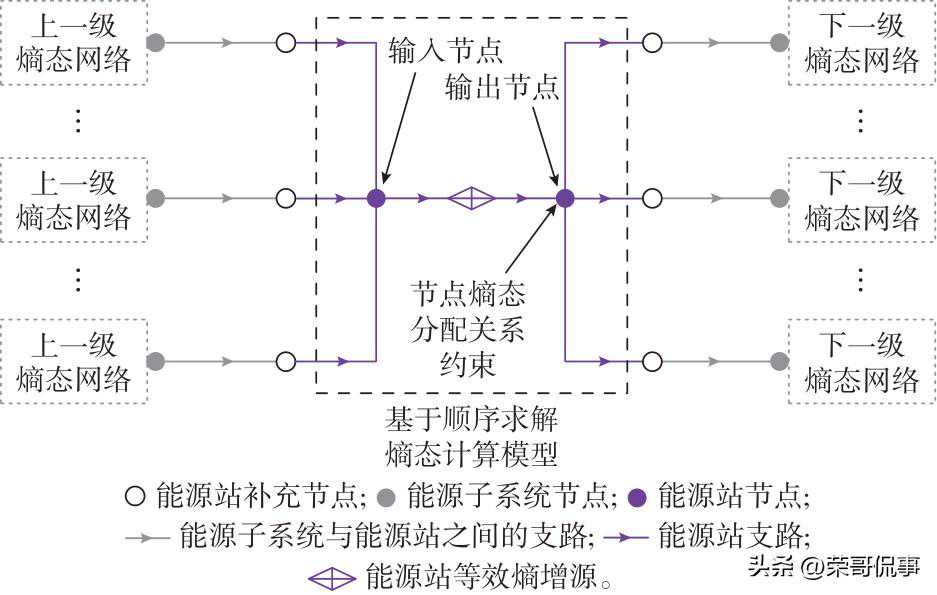
图3基于顺序求解的熵态计算模型中的ES熵态网络拓扑
asedonsequentialsolution
2.2各分系统熵态方程参数获取基于2.1节定义的各分系统熵态网络,可根据1.2节至1.4节确定部分熵态方程参数。以下重点讨论特殊熵态参数的获取方法。
顺序求解的思路是将熵增流交互部分的结果作为已知量代入下一级熵态网络的熵态方程中,直到完成全部的分系统熵态计算。在上一级熵态方程结果中,提取负荷熵增列向量中表达“注入下一级熵态网络的熵增流”的元素,代入下一级熵态方程作为节点注入熵增流列向量中表达“由上一级熵态网络注入的熵增流”的元素。
对于接入可再生能源设备的ES,其产生的熵增包含能源转化环节㶲损对应的传统热力学熵增ΔSh,ESΔ�h,ES和可再生能源设备导致的信息学等效热力学熵增ΔSi,ESΔ�i,ES,ES等效熵增源ΔSESΔ�ES为ES支路熵增源列向量ΔSESΔ�ES中内部支路对应的元素,可基于IES熵态机理模型计算如下:
ΔSES=ΔSh,ES+ΔSi,ES=ΔeESTa+pi,ESfi,ESTaΔ�ES=Δ�h,ES+Δ�i,ES=Δ�ES�a+�i,ES�i,ES�a
(29)
式中:ΔeESΔ�ES为ES能源转化环节产生的㶲损;pi,ES�i,ES为ES可再生能源设备的信息势;fi,ES�i,ES为ES可再生能源设备的信息流。
对于接入可再生能源发电设备的电力系统,不确定性导致的信息学等效热力学熵增以节点注入熵增流的形式注入电力系统熵态网络。因此,对于可再生能源接入的电力节点ne�e,需要计算对应元素,具体方法如下。
电力系统节点注入熵增流列向量ΔSin,eΔ�in,e中对应元素ΔSin,e,neΔ�in,e,�e即为该电源产生的信息学等效热力学熵增,由不确定熵态机理模型计算,如式(30)所示。
ΔSin,e,ne=pin,e,nefin,e,neTaΔ�in,e,�e=�in,e,�e�in,e,�e�a
(30)
式中:pin,e,ne�in,e,�e和fin,e,ne�in,e,�e分别为节点ne�e对应的可再生能源出力的信息势和信息流。
对于中压天然气系统,可以忽略气损失、气质改变、管存效应等条件[19-20],此时天然气网表现为无㶲损系统[7]。由式(13)可知,天然气支路熵增源列向量ΔSh,gΔ�h,g可由天然气支路㶲损ΔegΔ�g计算[7],由于天然气系统表现为无㶲损系统,此时ΔegΔ�g中元素均为0,ΔSh,gΔ�h,g中的元素也均为0。
根据1.2节可构建各分系统的熵态网络节点-支路关联矩阵。对于电力、天然气系统熵态网络,其拓扑结构与㶲流模型网络结构一致,故可以直接采用㶲流计算模型的节点-支路关联矩阵[8]。
对于热力系统熵态网络,其拓扑结构为基于㶲流模型的双层对称网络结构扩充而得的单层网络。考虑到热力系统㶲流模型供水网节点-支路关联矩阵已包含热力系统拓扑结构的关键信息,本文提出一种利用热力系统㶲流模型供水网节点-支路关联矩阵构建热力系统熵态网络节点-支路关联矩阵的方法,以提升应用效率。
定义热力节点-支路关联矩阵为Ah�h,维数为(2nh,n+nh,L)×(2nh,b+2nh,L)(2�h,n+�h,L)×(2�h,b+2�h,L),表示热力系统节点与支路之间的互联关系。下文将介绍Ah�h中各部分的主要构成子矩阵。
定义供水网络的节点-支路关联矩阵为As�s,维数为nh,n×nh,b�h,n×�h,b,与㶲流计算模型一致,用于表示供水节点与供水支路的互联情况,如式(31)所示。若某供水节点ih�h流向供水支路jh�h,则As�s中ih�h行jh�h列的元素为1。同理,当矩阵中某元素为-1时,表示对应供水节点与支路存在支路流向节点的关系。
As(ih,jh)=⎧⎩⎨⎪⎪1−10支路jh流入节点ih节点ih流向支路jh节点ih与支路jh无互联�s(�h,�h)=1支路�h流入节点�h-1节点�h流向支路�h0节点�h与支路�h无互联
(31)
式中:ih�h为1至nh,b�h,b间的任意正整数;jh�h为1至nh,n�h,n间的任意正整数。
定义回水网络的节点-支路关联矩阵为−As-�s,维数为nh,n×nh,b�h,n×�h,b,与㶲流计算模型一致。由于供回水网络拓扑结构一致,具有对称性,并且对称支路中的水流方向相反。因此,−As-�s即可表征热力回水节点与回水支路之间的互联关系。
定义nh,L�h,L个热力负荷标识列向量为Lh,i�h,�,ihL�hL为1至nh,L�h,L间的任意正整数,所有Lh,i�h,�维数均为nh,n�h,n,反映供水节点与负荷进水支路的互联情况,如式(32)所示。
Lh,ihL(ih)=⎧⎩⎨⎪⎪10供水网络节点ih向负荷i的流入负荷支路注入熵增流其他�h,�hL(�h)=1供水网络节点�h向负荷�的流入负荷支路注入熵增流0其他
(32)
若第ih�h个供水节点向第ihL�hL个热力负荷进水支路注入熵增流,则Lh,i�h,�中的第ih�h个元素为1,其余元素为0。因此,Lh,i�h,�为仅有一个非零元素1的列向量,−Lh,i-�h,�即可表征热力回水节点与负荷出水支路之间的互联关系。
定义负荷单位矩阵为Eh,L�h,L,维数为nh,L�h,L,表征热力负荷出口节点与负荷进水支路的互联关系。Eh,L�h,L第ihL�hL行第ihL�hL列元素为1表示第ihL�hL个负荷进水支路向第ihL�hL个负荷出口节点注入熵增流。−Eh,L-�h,L可表征热力负荷出口节点与负荷出水支路间的互联关系。−Eh,L-�h,L第ihL�hL行第ihL�hL列元素为-1表示第ihL�hL个负荷出口节点向第ihL�hL个负荷出水支路注入熵增流。
由上述As�s、Lh,i�h,�、Eh,L�h,L构成Ah�h,表示为:
Ah=⎡⎣⎢⎢As00−As0−Lh,10⋯⋯−Lh,nh,L00Lh,1⋯⋯0Lh,nh,LEh,L−Eh,L⎤⎦⎥⎥�h=�s00-�s-�h,1⋯-�h,�h,L0⋯00⋯0�h,1⋯�h,�h,L0�h,L-�h,L
(33)
Ah�h左上角部分为As�s和−As-�s构成的分块对角矩阵,维数为2nh,n×2nh,b2�h,n×2�h,b,反映供、回水网节点与支路的互联关系;右上角部分维数为2nh,n×2nh,L2�h,n×2�h,L,反映供、回水网节点与负荷支路的互联关系;右下角部分维数为nh,n×2nh,L�h,n×2�h,L,反映负荷出口节点与负荷支路的互联关系;左下角部分为0矩阵,反映负荷出口节点与供、回水支路无互联关系。
将Ah�h中-1元素置0可得热力流入节点-支路关联矩阵Ah,+�h,+,将−Ah-�h中-1元素置0可得热力流出节点-支路关联矩阵Ah,−�h,-,二者维数均为(2nh,n+nh,L)×(2nh,b+2nh,L)(2�h,n+�h,L)×(2�h,b+2�h,L)。
2.3基于顺序求解的熵态计算模型求解流程基于顺序求解的IES熵态计算模型求解流程为:根据㶲流传播方向,顺序求解各分系统熵态计算模型,期间将注入下级网络的熵增流代入下级网络熵态计算模型,最终得到所有系统的熵态分布。
ES作为多能耦合的关键环节,对求解顺序起决定性作用。因此,需要以ES为中心,根据㶲流模型确定ES的上级网络,先求解上级网络熵态方程,将上级网络注入ES的熵增流作为ES熵态方程的节点注入熵增流,进而求解ES熵态分布,再将ES注入下级网络的熵增流代入下级网络熵态方程。基于顺序求解的熵态计算模型流程图如图4所示。
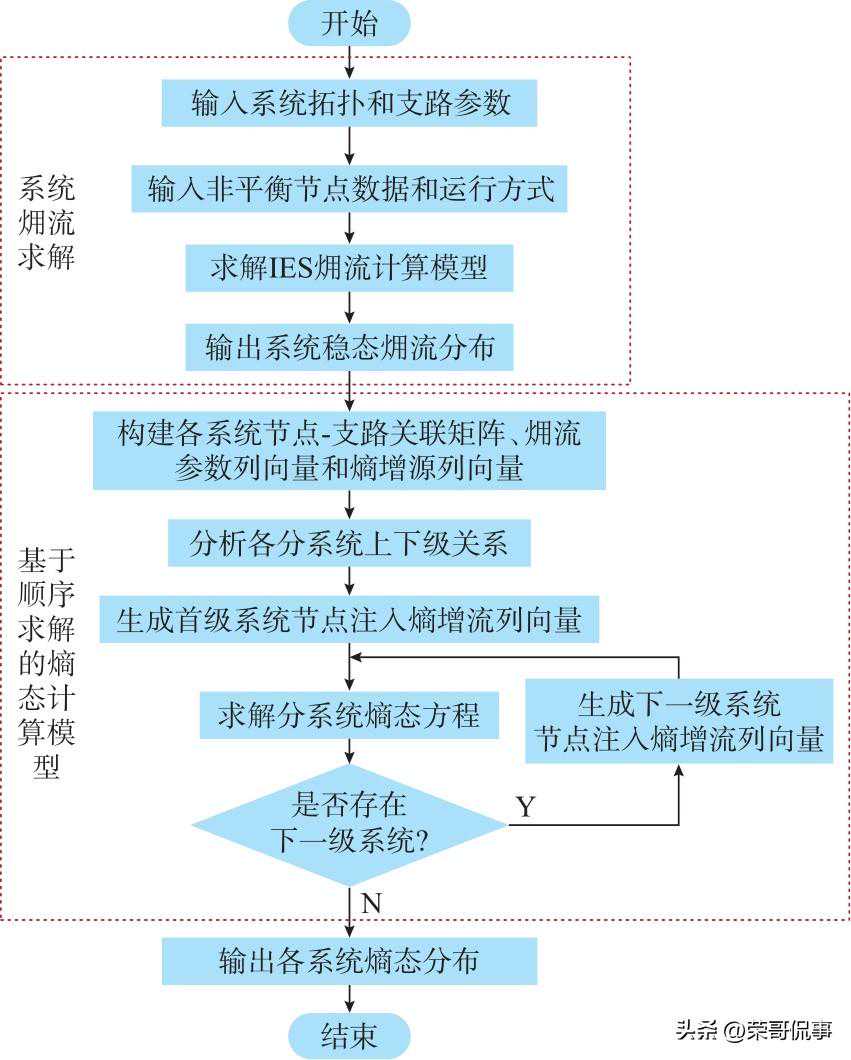
图4基于顺序求解的IES熵态计算模型流程图
ution
3基于联立求解的熵态计算模型构建基于联立求解的熵态计算模型的关键在于利用简洁ES熵态模型连接各能源子系统熵态网络,形成全系统熵态网络,直接求解全系统熵态方程进而获取熵态分布。采用的ES模型为2节点1支路1熵增源的简洁结构,在熵态网络中体现为一个具有熵增的“广义节点”,本文称之为“大节点”模型,如图5所示。
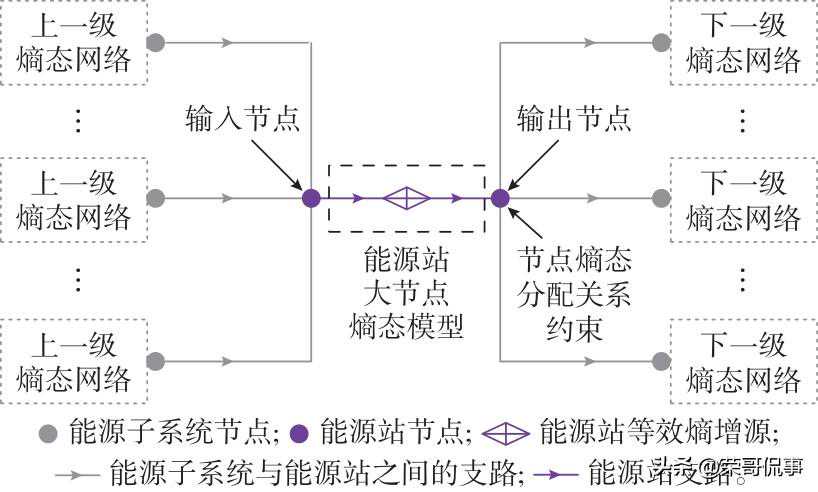
图5基于联立求解的熵态计算模型中ES示意图
taneoussolution
3.1全系统熵态网络结构定义以顺序求解熵态网络的方法定义各能源子系统熵态网络,并通过大节点ES模型的输入、输出支路连接各能源子系统熵态网络,形成IES全系统熵态网络。
设IES中存在电力、热力、天然气和nES�ES个ES,其中,电力系统网络为ne,n�e,n节点ne,b�e,b支路结构;天然气系统网络为ng,n�g,n节点ng,b�g,b支路结构;热力系统为对称供回水网络,存在nh,L�h,L个热力负荷,供水网为nh,n�h,n节点nh,b�h,b支路结构;第n'ES�ES'个ES存在ninn'ES��ES'in输入noutn'ES��ES'out输出,n'ES�ES'为1至nES�ES任意正整数。
在联立求解计算模型中,ES由输入、输出2个节点及内部支路构成。以第n'ES�ES'个ES为例,电、气、热系统输入该ES的熵增流经ninn'ES��ES'in个输入支路注入输入节点,经等效熵增源后,由输出节点流向noutn'ES��ES'out个输出支路,最终流向其他系统。
因此,ES部分为IES的熵态计算模型增加了2nES2�ES个节点、nES,b�ES,b个支路,其中,nES,b�ES,b可表示为:
nES,b=∑n'ES=1nESninn'ES+∑n'ES=1nESnoutn'ES�ES,b=∑�ES'=1�ES��ES'in+∑�ES'=1�ES��ES'out
(34)
综上,IES全系统熵态网络为nIES,n�IES,n节点nIES,b�IES,b支路结构。其中,nIES,n�IES,n为IES总节点数,即各系统节点总数;nIES,b�IES,b为总支路数,即各系统支路总数,表示如下:
nIES,n=ne,n+ng,n+2nh,n+nh,L+2nES�IES,n=�e,n+�g,n+2�h,n+�h,L+2�ES
(35)
nIES,b=ne,b+ng,b+2nh,b+2nh,L+nES,b�IES,b=�e,b+�g,b+2�h,b+2�h,L+�ES,b
(36)
3.2全系统熵态方程参数获取根据3.1节定义的全系统熵态网络以及系统稳态㶲流分布,可构建IES全系统熵态方程。对于方程的参数列向量,规定其中元素的排列顺序遵循电力、天然气、热力、ES的排序原则,这一原则同样适用于IES全系统节点-支路关联矩阵。
IES全系统节点-支路关联矩阵AIES�IES的维数为nIES,n×nIES,b�IES,n×�IES,b,如式(37)所示。其左上角部分反映电力、天然气、热力系统节点与支路的连接关系;右上角部分反映ES输入、输出支路与电、气、热系统节点的连接关系;右下角部分反映ES输入、输出节点与输入、输出支路的连接关系;左下角部分为0矩阵,反映ES输入、输出节点与电、气、热系统支路无连接关系。
AIES=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢Ae000Ag000Ah0Anet1⋯Anetn'ES⋯AnetnESAes1⋮0⋯Aesn'ES⋯0⋮AesnES⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥�IES=�e000�g000�h�1net⋯��ES'net⋯��ESnet0�1es⋯0⋮��ES'es⋮0⋯��ESes
(37)
式中:Ae�e为电力系统节点-支路关联矩阵,维数为ne,n×ne,b�e,n×�e,b;Ag�g天然气系统节点-支路关联矩阵,维数为ng,n×ng,b�g,n×�g,b;Anet1�1net至AnetnES��ESnet为电、气、热节点-ES输入、输出支路关联矩阵,其中,第n'ES�ES'个ES对应的Anetn'ES��ES'net的维数为(ne,n�e,n+ng,n�g,n+2nh,n2�h,n+nh,L�h,L)××(ninn'ES��ES'in+noutn'ES��ES'out+11);Aes1�1es至AesnES��ESes为ES节点-支路关联矩阵,其中,第n'ES�ES'个ES对应的Aesn'ES��ES'es的维数为2×(ninn'ES��ES'in+noutn'ES��ES'out+1)。
Ae�e、Ag�g、Ah�h、Anetn'ES��ES'net、Aesn'ES��ES'es中的元素与IES网络节点、支路的对应关系如下:
1)Ae�e、Ag�g中各元素反映电、气节点与支路之间的连接关系,其中,各行分别对应电、气节点,各列对应电、气支路;Ah�h中各元素反映热力节点与支路之间的连接关系,其中,各行分别对应供水节点、回水节点、负荷出口节点,各列对应供水支路、回水支路、负荷进水支路、负荷出水支路。
2)Anetn'ES��ES'net中各元素反映电、气、热节点与ES输入、输出支路之间的连接关系,其中,各行分别对应电、气、热节点,各列对应ES输入、输出支路和ES内部支路。
3)Aesn'ES��ES'es中各元素反映各ES输入、输出节点与输入、输出支路之间的连接关系,各行分别对应各ES输入、输出节点,各列对应ES输入、输出支路和ES内部支路。
得到AIES�IES后,将其中-1元素置0,得到IES全系统流入节点-支路关联矩阵AIES,+�IES,+,反映各节点与流入该节点的支路之间的连接关系;将−AIES-�IES中-1元素置0,得到IES全系统流出节点-支路关联矩阵AIES,−�IES,-,反映各支路与流出节点的连接关系。
3.3基于联立求解的熵态计算模型求解流程根据3.1节和3.2节可获取IES全系统熵态方程参数列向量和关联矩阵,求解熵态方程便可获得IES全系统熵态分布。基于联立求解的熵态计算模型流程图如图6所示。

图6基于联立求解的熵态计算模型流程图
tion
4两种熵态计算模型的异同和适用性分析根据两种熵态计算模型的建模框架、熵态方程求解流程以及方程参数的特点,总结出以下相同特征:
1)各类熵增环节的传统热力学熵增和信息学等效热力学熵增的计算方法一致,包括支路熵增源、可再生能源信息学等效热力学熵增、负荷信息学等效热力学熵增、ES等效熵增源等,初始输入均来自IES㶲流模型以及源荷历史数据。
2)获取系统熵态分布的过程分为㶲流计算和熵态计算两部分,熵态计算模型的求解过程主要为矩阵与向量相乘的顺序结构,㶲流计算模型的求解过程存在大量循环结构。因此,当系统规模足够大时,熵态计算模型求解过程本身的时间复杂度可以忽略,即系统熵态分布算法的性能由㶲流计算部分决定。
3)相比根据熵态机理模型逐一节点支路递推计算的方法,熵态计算模型为矩阵化方程组求解的计算过程,故更适合采用计算机对大规模系统进行熵态分析。
4)熵态方程参数矩阵中,非零项总数与节点数和支路数线性相关,总项数与节点数和支路数的乘积线性相关。因此,当系统规模增大时,非零项占总项数的比例呈降低趋势,节点-支路关联矩阵更趋近于稀疏矩阵,两种熵态计算模型的总体运算耗时并不会随系统的规模增加呈现出求解时长激增的情况。
两种熵态计算模型最大的区别在于能量转化环节,即ES建模存在差异,导致适用性不同:
1)顺序求解中ES部分具有独立的熵态网络,可采用更为精细化的ES模型以提升熵态建模的精确程度,例如:采用非线性或基于数据驱动的黑箱化模型;联立求解中ES结构采用精简的“大节点”模型,仅表达ES内部两种熵增机理和输出熵增流的分配机制,相比于顺序求解,其不适合于精细化ES建模。
2)联立求解中ES采用“大节点”的模型,含有多个能源网络的IES可整合为一个熵态网络进行计算。因此,基于联立求解的熵态计算模型更适用于多个ES互联的IES熵态分析。
5算例分析5.1算例介绍本文构建了一个基于典型IES的算例测试系统,如附录A图A1所示。该系统包括3个子系统,即6节点电力系统、7节点天然气系统和5节点热力系统[21-22]。为计及能量转化环节对系统熵态分布情况的影响,算例系统中配备了两个ES,如附录A图A5所示。IES㶲流模型和熵态模型的环境温度设为10℃。6节点电力系统是基于IEEE33节点系统修改的,电压等级为12.66kV,在电力节点E2和E3处分别接入分布式PV和风力机(windturbine,WT),以考虑可再生能源不确定性导致的信息学等效热力学熵增对IES熵态分布情况的影响。7节点天然气系统的气源气压为0.5MPa,天然气的热值和理论燃烧温度分别为45.75MJ/m3和1973℃。热力系统的相关参数是基于典型系统数据进行修改的。两个ES为供热系统提供热能,热源出水温度设为100℃,负荷出水温度为50℃。
算例配置的2个典型ES中,ES1配备了一台CHP和一台GB,CHP的气转电和气转热效率分别为ηCHPg2e=0.3�g2eCHP=0.3、ηCHPg2h=0.4�g2hCHP=0.4,GB的气转热效率ηGBg2h=0.85�g2hGB=0.85[23]。ES1输入端连接电力网络节点E6、天然气网络节点G6,输出端连接热力网络节点H1,同时为热力系统和电力系统提供热能和电能。ES2配备了一台GB和一台电锅炉(electricboiler,EB),能源转化效率分别为ηGBg2h=0.85�g2hGB=0.85和ηEBe2h=0.95�e2hEB=0.95[23]。ES2输入端连接电力网络节点E5、天然气网络节点G7,输出端连接热力网络节点H2,为热力系统提供热能。针对源荷不确定性导致的信息学等效热力学熵增,本文基于源荷全年逐时数据,以文献[7]中弱预测场景为例,构建源荷熵态模型。
5.2两种模型的参数与结果根据算例系统分别构建两种计算模型,其已知参数与计算结果的向量形式见附录B表B1和表B2。根据上述参数与结果,绘制两种熵态计算模型的熵态网络如图B1和图B2所示。根据㶲流的流向逐一计算所有支路熵增流和节点熵增,所得结果与上述结果一致,可验证两种熵态计算模型的正确性和等效性。
5.3整体(源荷)熵态平衡关系检验各类熵增源产生的熵增在熵态网络中以熵增流向负荷传播。因此,熵增源总熵增与负荷总熵增应当完全一致,即系统满足整体熵态平衡关系。算例系统熵增源总熵增为5.3118kW/K,补充负荷节点熵增总和为5.3114kW/K,在计算误差小于万分之一的范围内满足上述系统熵增的整体熵态平衡关系,具体统计与分析数据的如附录C表C1所示。
5.4(局部)节点熵态平衡关系检验由IES熵态机理模型可知:一个封闭或孤立的能源系统熵态模型内,各节点总输入与总输出熵增流相等,即系统节点满足(局部)节点熵态平衡关系。检验系统中各节点的总输入与总输出熵增流,可发现上述关系成立,具体统计与分析数据如附录C表C2所示。
5.5(局部)节点熵态分配关系检验由IES熵态机理模型可知:系统节点熵增流输出遵循(局部)节点熵态分配关系。对于输出总熵增流非零的节点,各输出熵增流与总输出熵增流的比值应等于各输出㶲流与总输出㶲流的比值;对于输出总熵增流为零的节点,各输出熵增流也应为零。经检验,各节点均满足上述关系。具体统计与分析数据见附录D。
6结语本文基于IES㶲流和熵态机理模型,根据节点熵态平衡与分配关系,提出了求解任意能源网络熵态分布的熵态方程;基于两种ES熵态模型,提出基于顺序求解和联立求解的IES熵态计算模型,用于求解IES熵态分布;讨论了两种计算模型的异同以及适用性;最后,通过算例验证两种计算模型的有效性。结果表明:
1)两种熵态计算模型均可求解IES支路熵增流、节点熵增以及负荷熵增,与熵态机理模型逐一递推方法所得结果一致。
2)顺序求解的熵态计算模型的电、气、热系统以及ES熵态模型求解彼此分立,更适用于精细化ES熵态模型和内部复杂ES的精细化熵态分析。求解过程需要根据㶲流流向判别各分系统上下级关系,再进行顺序求解,当ES数量较大时,求解难度增加。
3)联立求解的熵态计算模型中,ES嵌于全系统熵态网络中,无须判别上下级关系,可直接求解全系统熵态方程,获取全系统熵态分布。因此,适用于存在多个ES的系统,但不适用于需要引入精细化ES熵态模型的系统。
4)考虑两种计算模型熵态方程中的节点-支路关联矩阵,定性分析矩阵稀疏程度和系统规模的关系,可知模型运算时长不随系统规模的增大而激增,且节点-支路关联矩阵的稀疏化降低了计算资源占用量,有利于模型规模化应用。
后续研究将从能量介质动态响应特性的角度,针对元件、单元、系统级别的熵态建模,开展不同时间和空间尺度下IES熵态机理与计算的研究,提升IES熵态理论的适用性。
附录附录A
图A1测试算例系统示意图
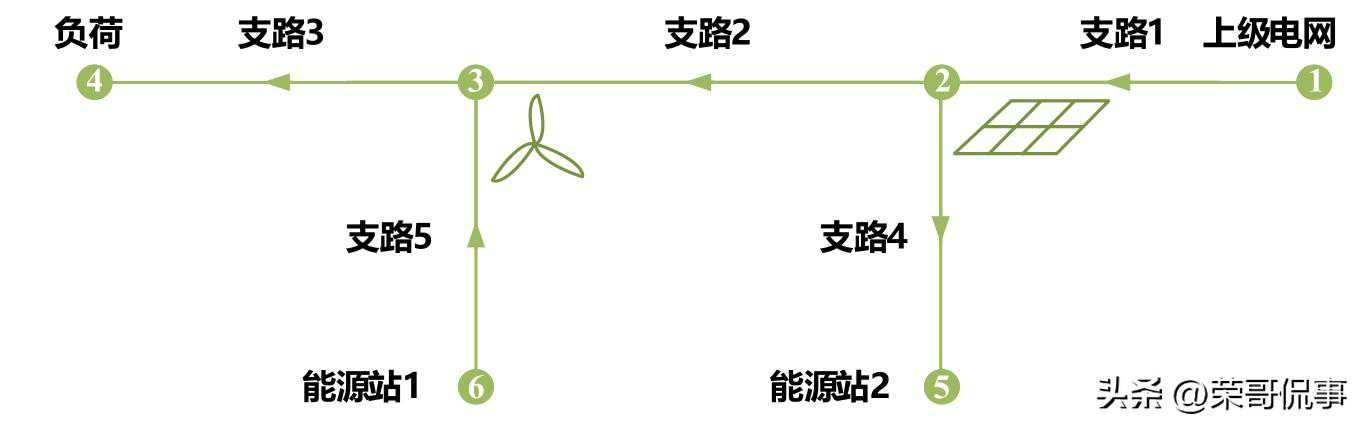
(a)算例IES电力系统示意图

(b)算例IES电力系统熵态网络示意图
图A2算例IES电力系统熵态计算模型示意图
mofcasestudyIES
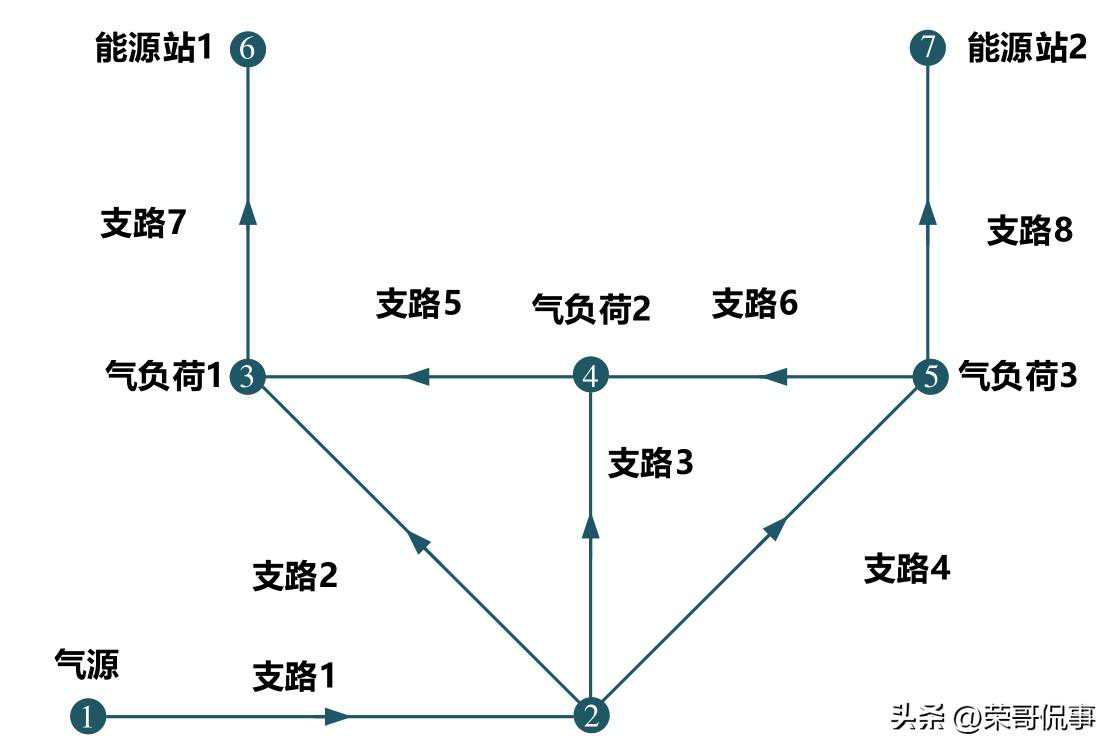
(a)算例IES天然气系统示意图

(b)算例IES天然气系统熵态网络示意图
图A3算例IES天然气系统熵态计算模型示意图
ystemofcasestudyIES
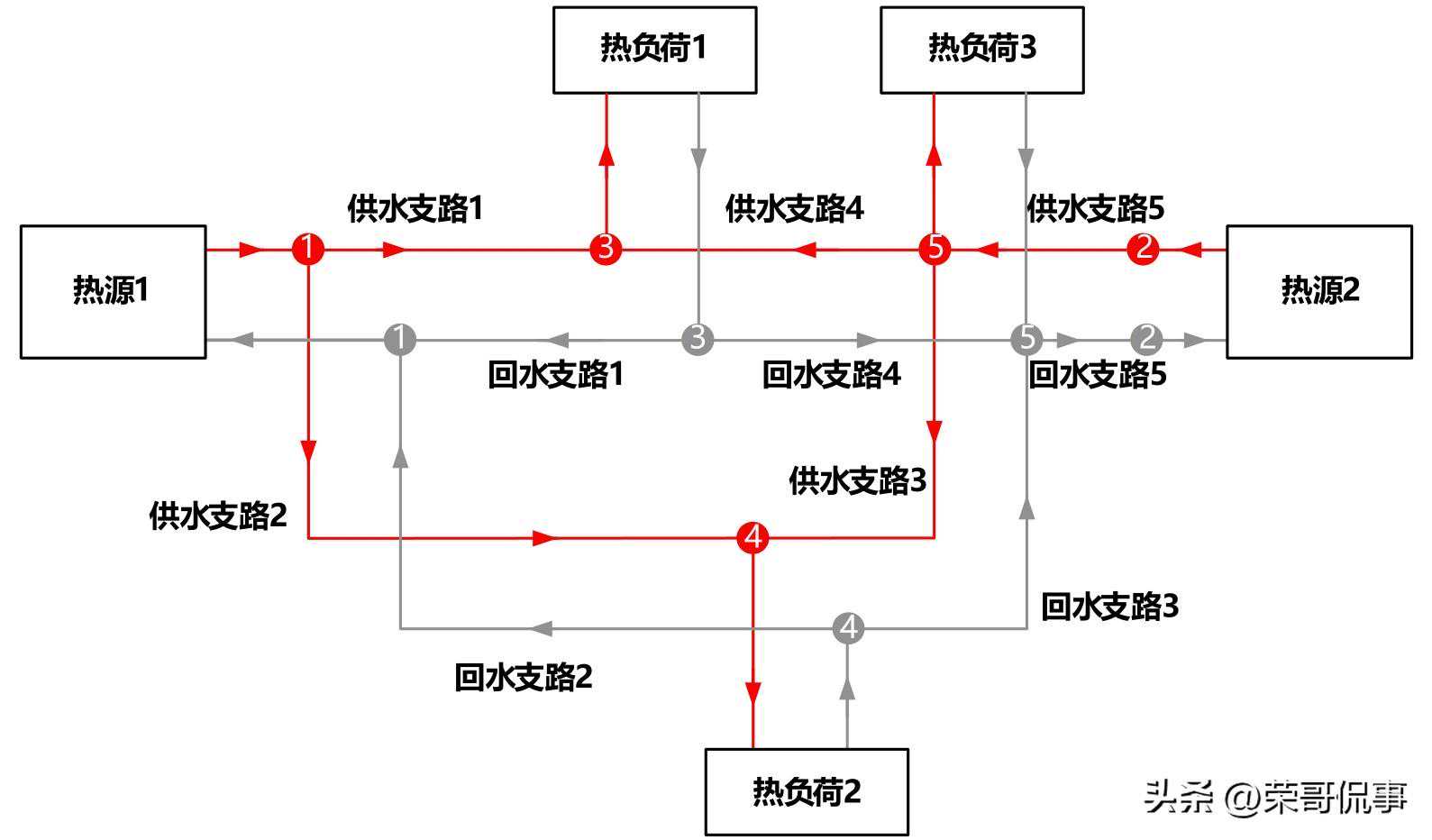
(a)算例IES热力系统示意图
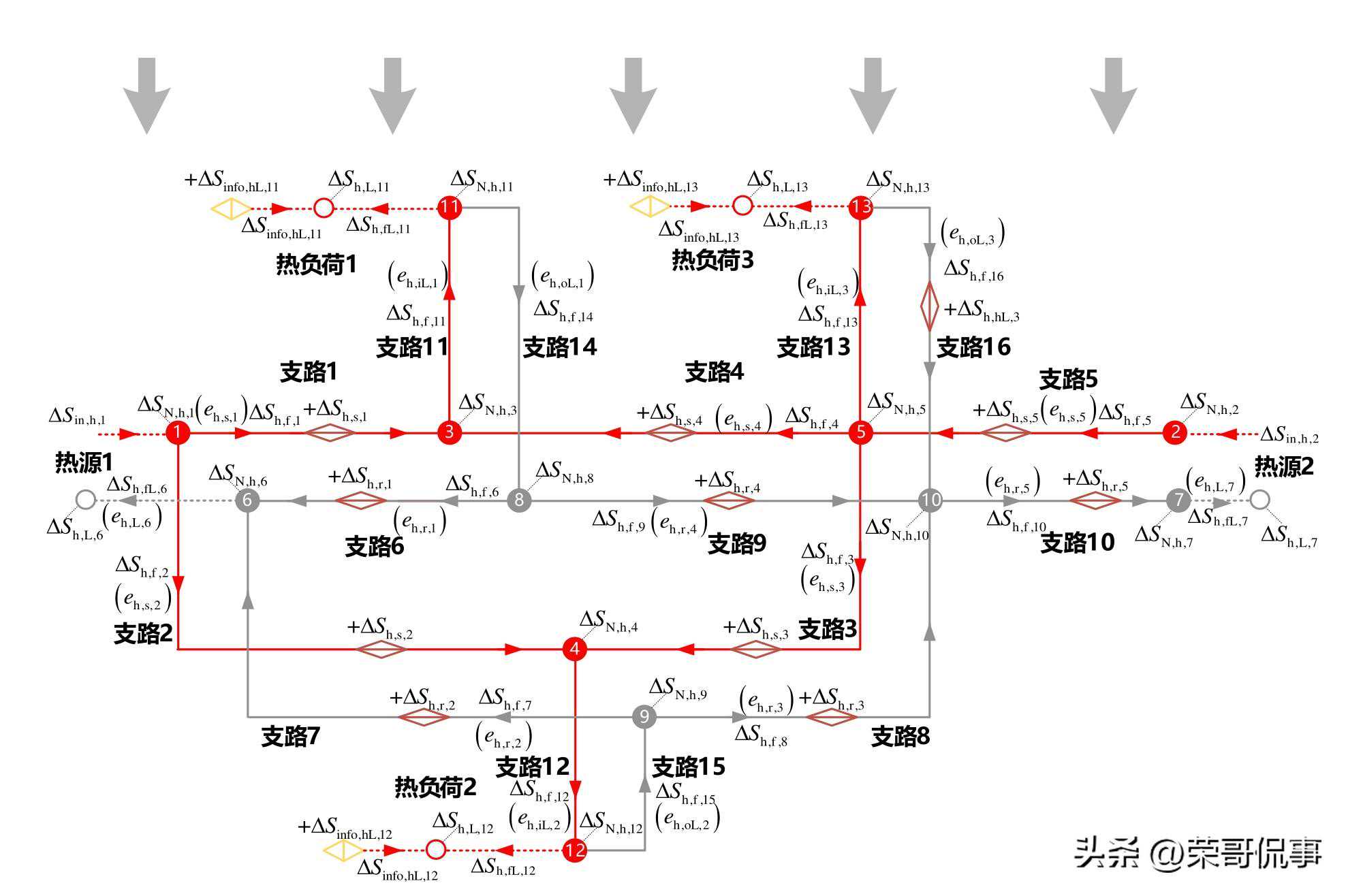
(b)算例IES热力系统熵态网络示意图
图A4算例IES热力系统熵态计算模型示意图
ofcasestudyIES
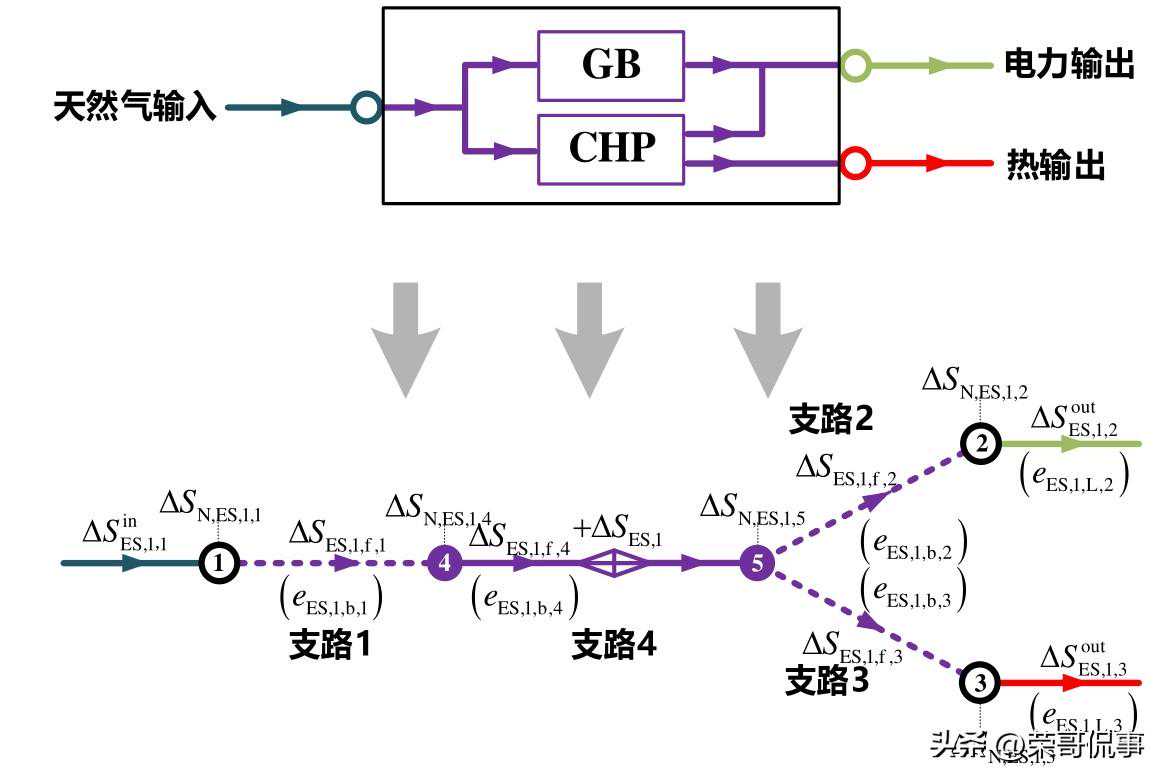
(a)算例IES的1号ES熵态计算模型示意图
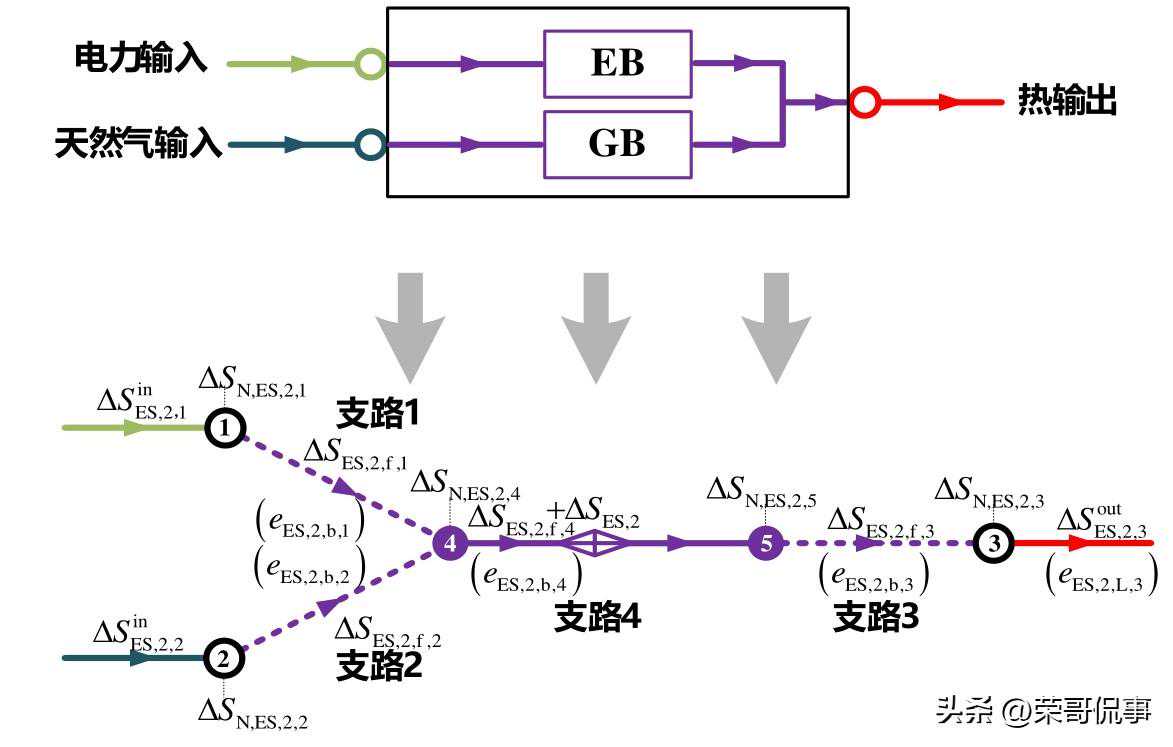
(b)算例IES的2号ES熵态计算模型示意图
图A5算例IES的ES熵态计算模型示意图
ionsofcasestudyIES
附录B表B1基于顺序和联立求解的熵态计算模型的输入参数
TableB1Inputparametersoftheentropystatecalculationmodelbasedonsequentialsolutionandsimultaneoussolution
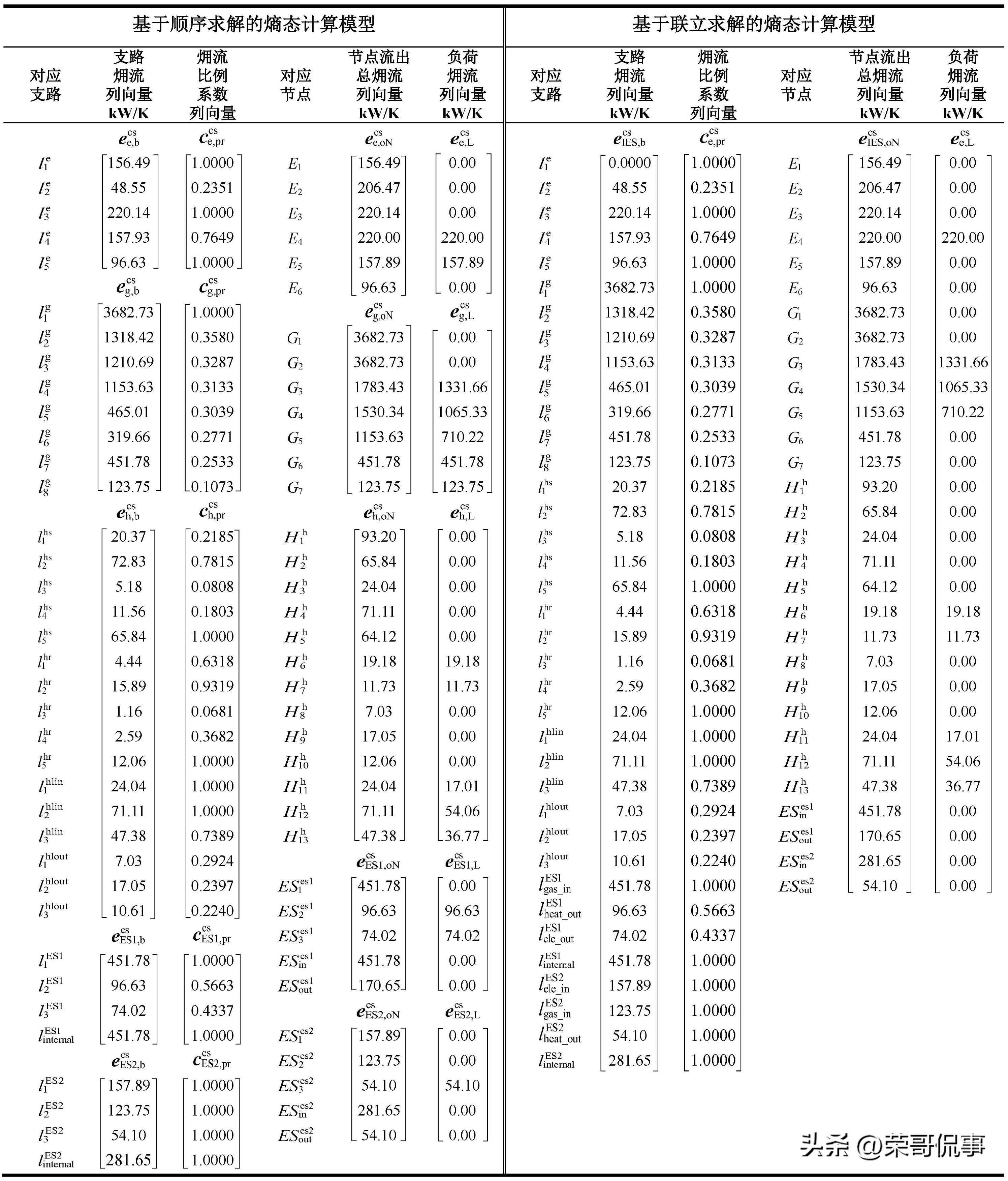
表B1展示了两种计算模型的㶲流初始输入列向量,其中:基于顺序求解的熵态计算模型输入列向量包括电力系统、天然气系统、热力系统、ES1、ES2的支路㶲流列向量ecse,b�e,bcsecsg,b�g,bcsecsh,b�h,bcsecsES1,b�ES1,bcsecsES2,b�ES2,bcs、节点总流出㶲流列向量ecse,oN�e,oNcsecsg,oN�g,oNcsecsh,oN�h,oNcsecsES1,oN�ES1,oNcsecsES2,oN�ES2,oNcs、负荷㶲流列向量ecse,L�e,Lcsecsg,L�g,Lcsecsh,L�h,LcsecsES1,L�ES1,LcsecsES2,L�ES2,Lcs、㶲流比例系数列向量ccse,pr�e,prcsccsg,pr�g,prcsccsh,pr�h,prcsccsES1,pr�ES1,prcsccsES2,pr�ES2,prcs;基于联立求解的熵态计算模型输入列向量包括:IES全系统支路㶲流列向量ecsIES,b�IES,bcs、节点总流出㶲流列向量ecsIES,oN�IES,oNcs、负荷㶲流列向量ecsIES,L�IES,Lcs、㶲流比例系数列向量ccsIES,pr�IES,prcs。
表B2基于顺序和联立求解的熵态计算模型的计算结果
TableB2Inputparameteroftheentropystatecalculationmodelbasedonsequentialsolutionandsimultaneoussolution
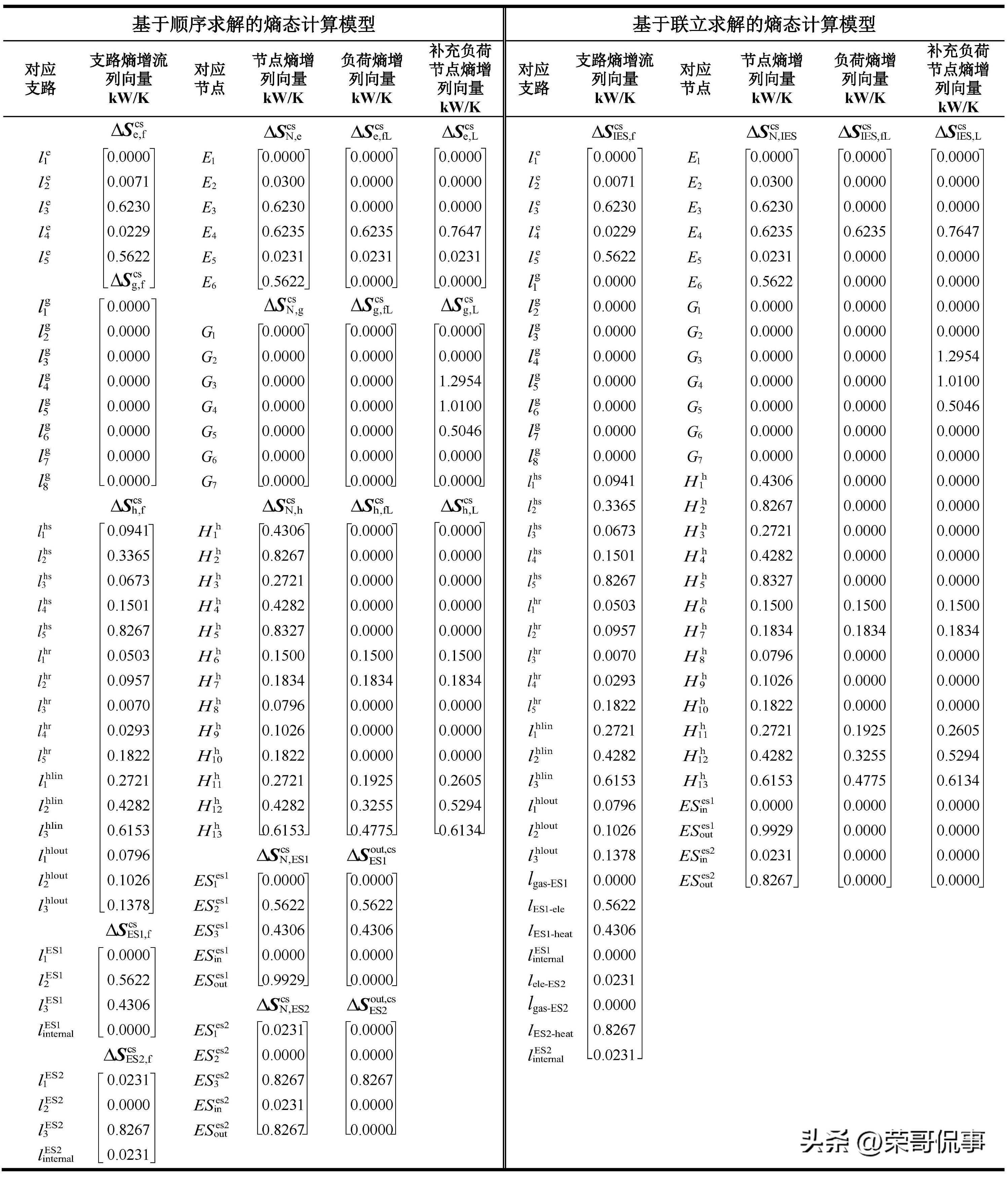
表B2展示了两种计算模型的计算结果,其中:基于顺序求解的熵态计算模型计算结果包括电力系统、天然气系统、热力系统、ES1、ES2的支路熵增流列向量ΔScse,fΔ�e,fcsΔScsg,fΔ�g,fcsΔScsh,fΔ�h,fcsΔScsES1,fΔ�ES1,fcsΔScsES2,fΔ�ES2,fcs、节点熵增列向量ΔScsN,eΔ�N,ecsΔScsN,gΔ�N,gcsΔScsN,hΔ�N,hcsΔScsN,ES1Δ�N,ES1csΔScsN,ES2Δ�N,ES2cs、负荷熵增列向量ΔScse,fLΔ�e,fLcsΔScsg,fLΔ�g,fLcsΔScsh,fLΔ�h,fLcsΔSout,csES1Δ�ES1out,csΔSout,csES2Δ�ES2out,cs、补充负荷节点熵增列向量ΔScse,LΔ�e,LcsΔScsg,LΔ�g,LcsΔScsh,LΔ�h,Lcs;基于联立求解的熵态计算模型计算结果包括:IES全系统支路熵增流列向量ΔScsIES,fΔ�IES,fcs、节点熵增列向量ΔScsN,IESΔ�N,IEScs、负荷熵增列向量ΔScsIES,fLΔ�IES,fLcs、补充负荷节点熵增列向量ΔScsIES,LΔ�IES,Lcs;
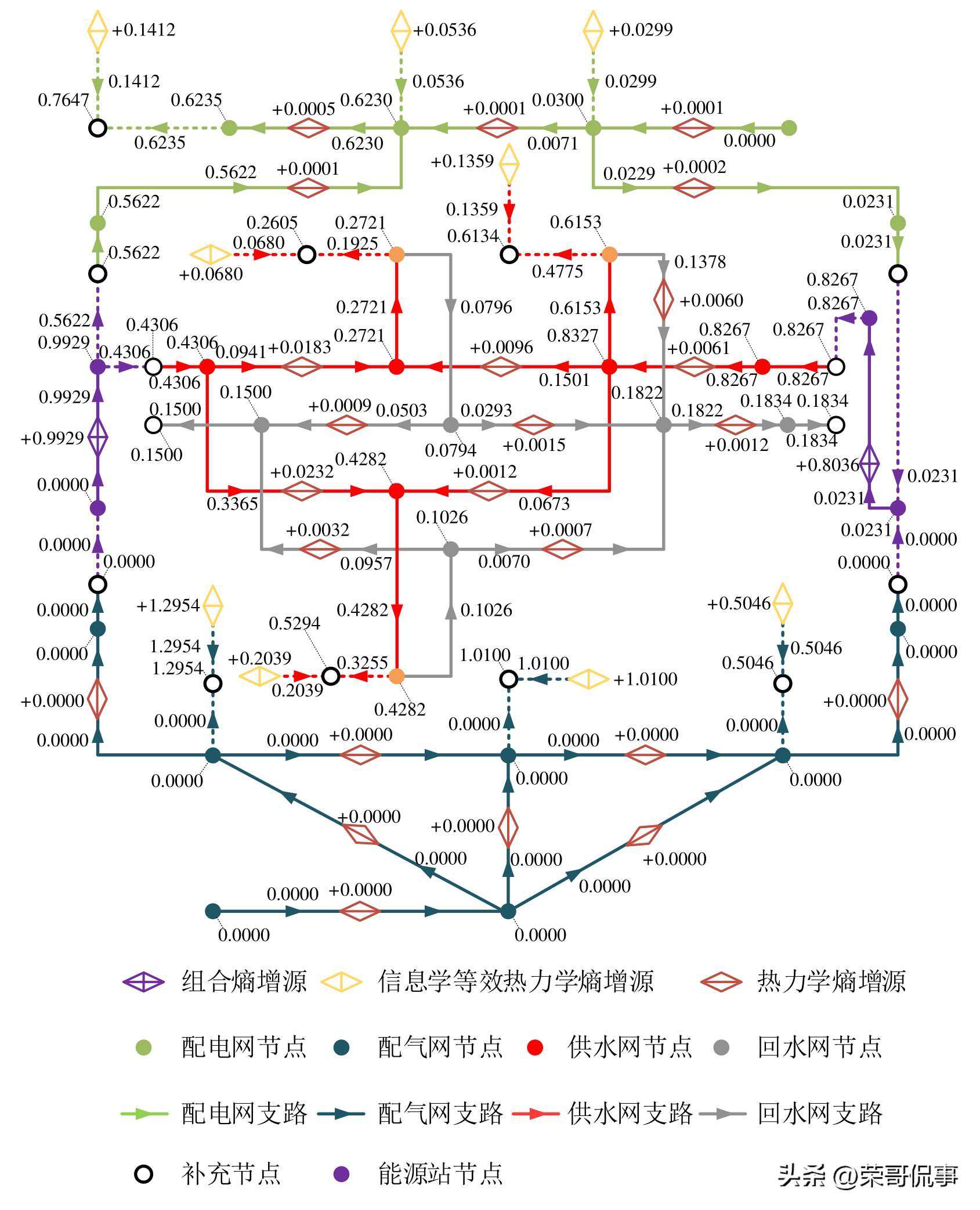
(a)基于顺序求解的熵态计算模型全系统示意图
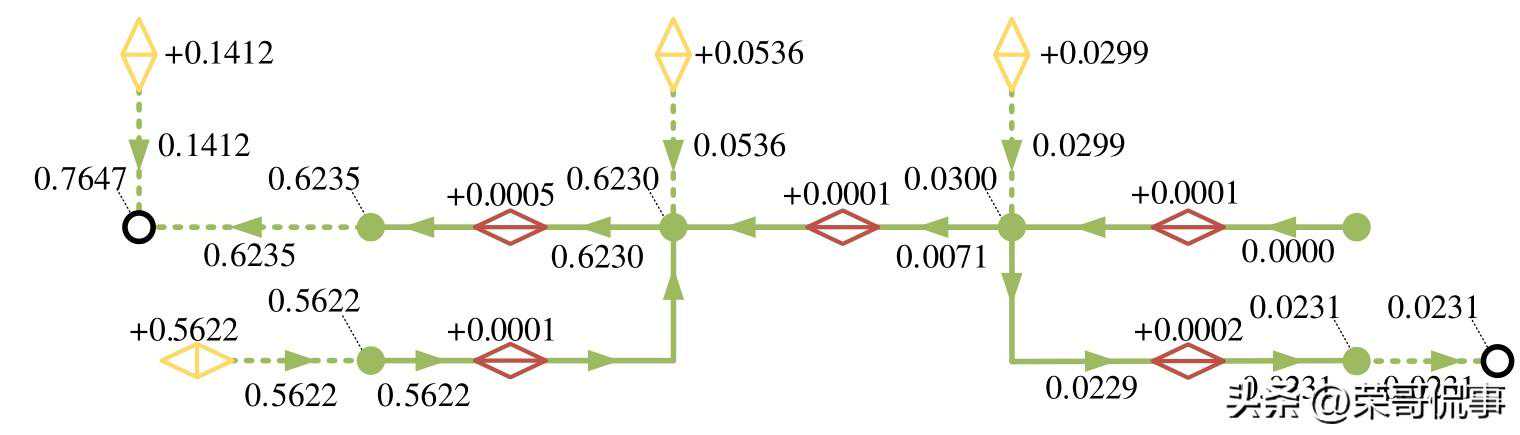
(b)基于顺序求解的熵态计算模型电力系统示意图
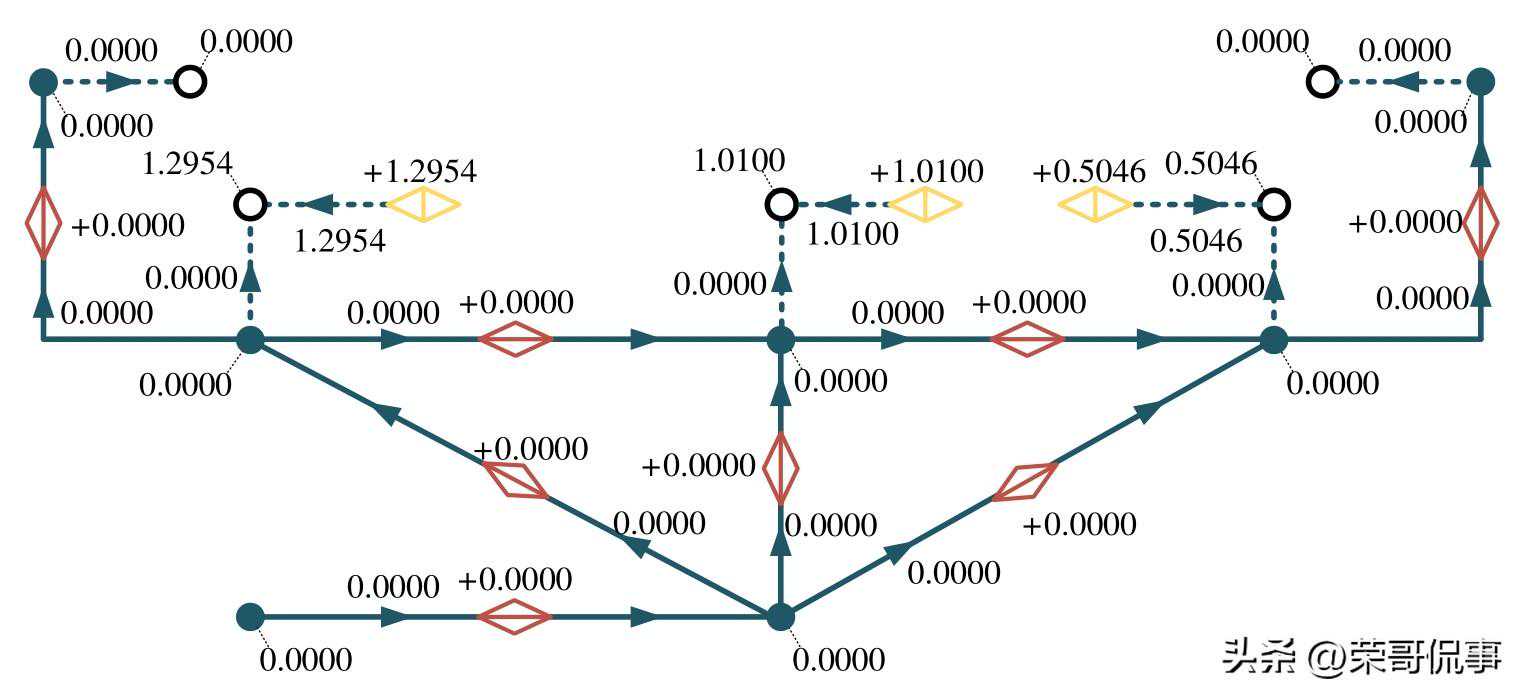
(c)基于顺序求解的熵态计算模型天然气系统示意图
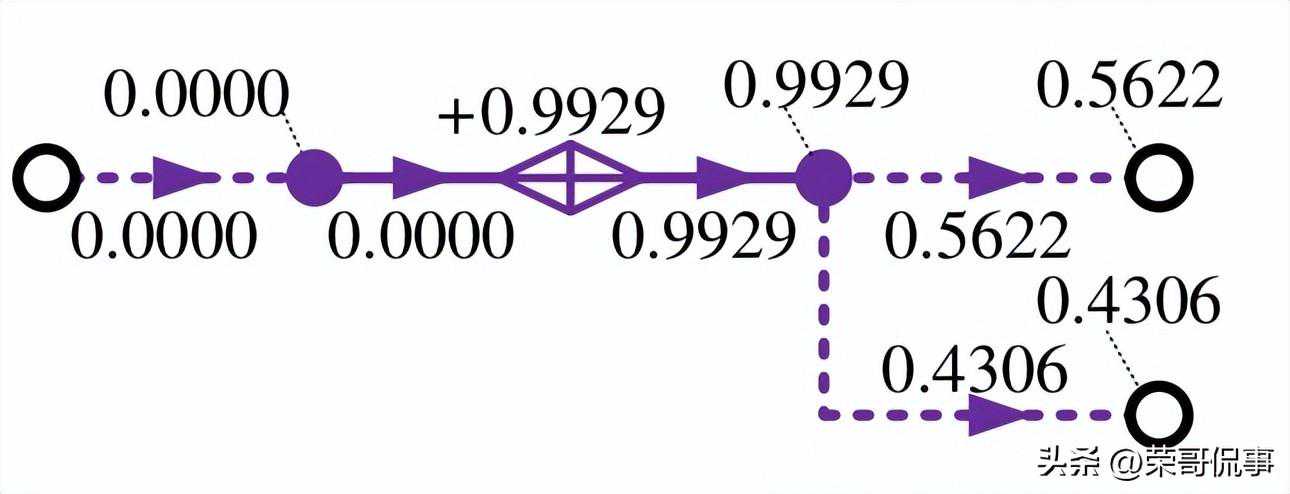
(d)基于顺序求解的熵态计算模型ES1示意图
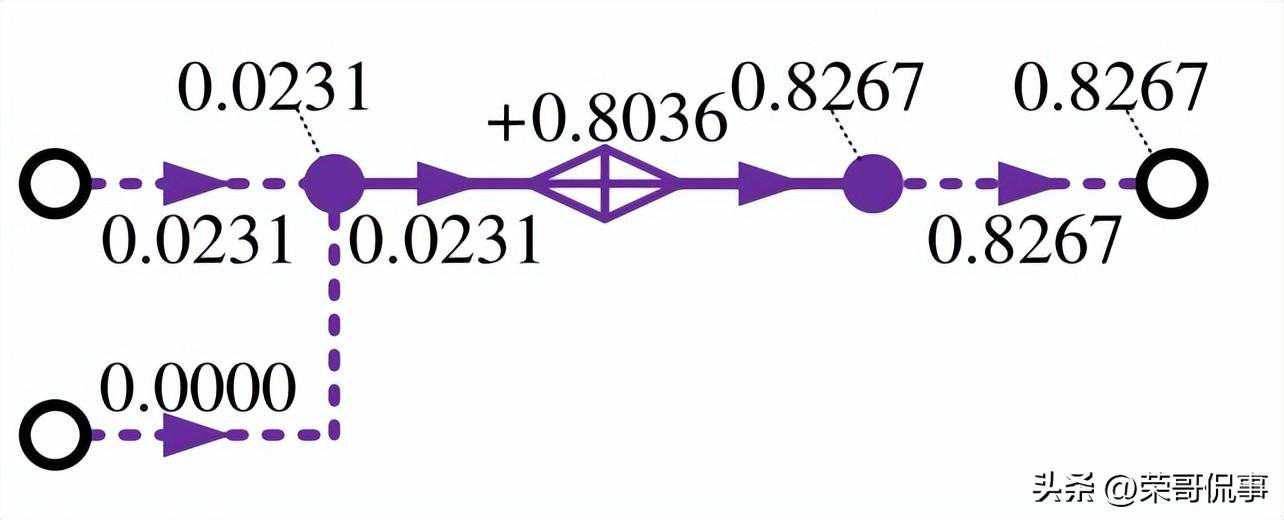
(e)基于顺序求解的熵态计算模型ES2示意图
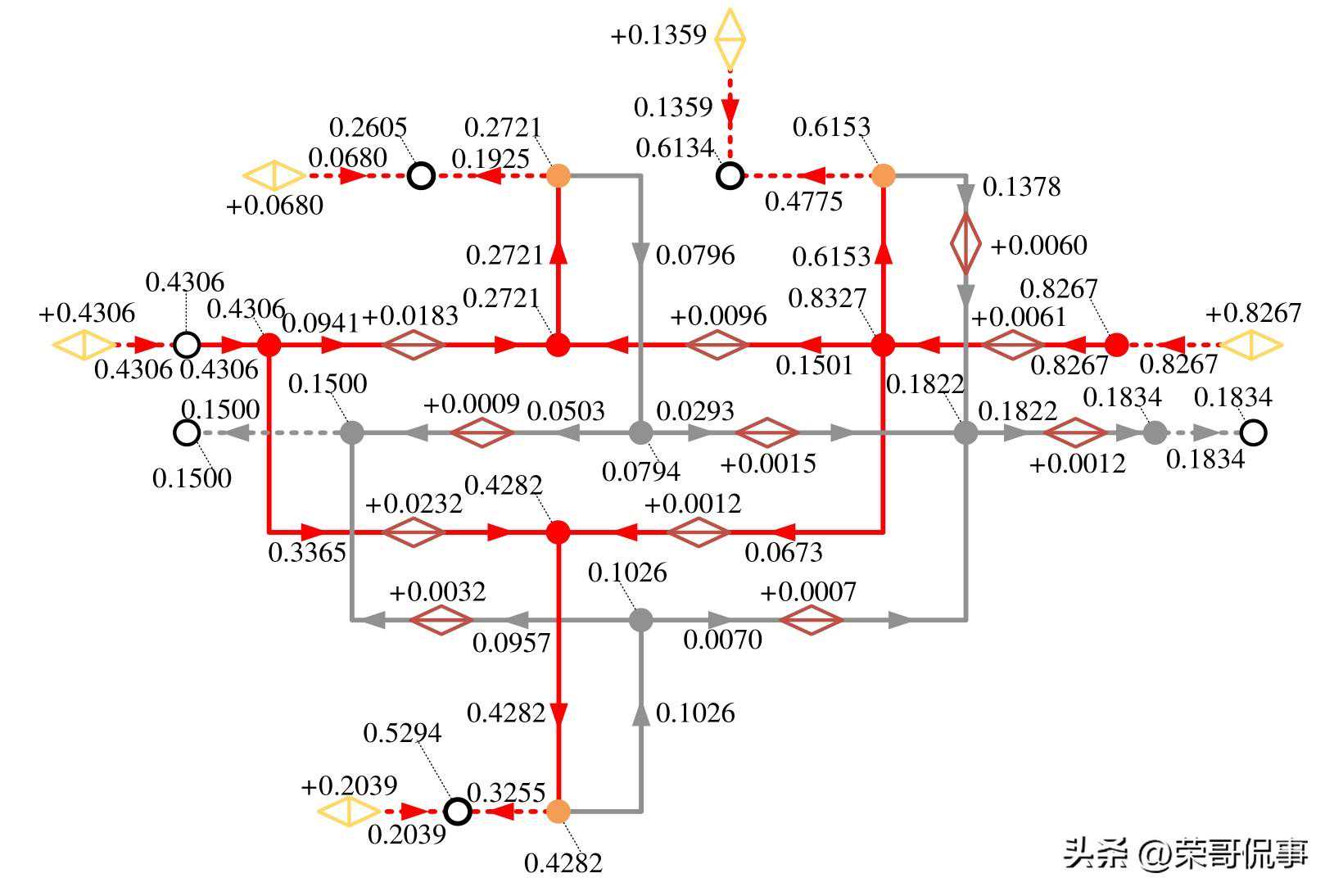
(f)基于顺序求解的熵态计算模型热力系统示意图
图B1基于顺序求解的熵态计算模型结果示意图
edonsequentialsolution

图B2基于联立求解的熵态计算模型结果示意图
edonsimultaneoussolution
图中:“数字”形式为支路熵增流大小,“+数字”形式为各类熵增源产生的熵增,带有指向节点虚线的“数字”为熵态网络节点熵增或各类补充节点熵增。
附录C表C1整体(源-荷)熵态平衡关系验证比较(以联立求解为例)
TableC1Verificationandcomparisonofoverallentropystatebalancerelationship(source-load)(simultaneoussolutionasexample)
熵增源产生熵增分布
负荷总熵增分布
类别
位置
熵增(kW/K)
位置
熵增(kW/K)
传统热力熵增(电力)
le1�1e
0.0001
E1�1
0.0000
传统热力熵增(电力)
le2�2e
0.0001
E2�2
0.0000
传统热力熵增(电力)
le3�3e
0.0005
E3�3
0.0000
传统热力熵增(电力)
le4�4e
0.0001
E4�4
0.7647
传统热力熵增(电力)
le5�5e
0.0001
E5�5
0.0000
传统热力熵增(天然气)
lg1�1g
0.0000
E6�6
0.0000
传统热力熵增(天然气)
lg2�2g
0.0000
G1�1
0.0000
传统热力熵增(天然气)
lg3�3g
0.0000
G2�2
0.0000
传统热力熵增(天然气)
lg4�4g
0.0000
G3�3
1.2954
传统热力熵增(天然气)
lg5�5g
0.0000
G4�4
1.0100
传统热力熵增(天然气)
lg6�6g
0.0000
G5�5
0.5046
传统热力熵增(天然气)
lg7�7g
0.0000
G6�6
0.0000
传统热力熵增(天然气)
lg8�8g
0.0000
G7�7
0.0000
传统热力熵增(热力)
lh1�1h
0.0183
Hh1�1h
0.0000
传统热力熵增(热力)
lh2�2h
0.0232
Hh2�2h
0.0000
传统热力熵增(热力)
lh3�3h
0.0012
Hh3�3h
0.0000
传统热力熵增(热力)
lh4�4h
0.0096
Hh4�4h
0.0000
传统热力熵增(热力)
lh5�5h
0.0061
Hh5�5h
0.0000
传统热力熵增(热力)
lh6�6h
0.0009
Hh6�6h
0.1500
传统热力熵增(热力)
lh7�7h
0.0032
Hh7�7h
0.1834
传统热力熵增(热力)
lh8�8h
0.0007
Hh8�8h
0.0000
传统热力熵增(热力)
lh9�9h
0.0015
Hh9�9h
0.0000
传统热力熵增(热力)
lh10�10h
0.0012
Hh10�10h
0.0000
传统热力熵增(热力)
lh11�11h
0.0000
Hh11�11h
0.2605
传统热力熵增(热力)
lh12�12h
0.0000
Hh12�12h
0.5294
传统热力熵增(热力)
lh13�13h
0.0000
Hh13�13h
0.6134
传统热力熵增(热力)
lh14�14h
0.0000
ESes11��1es1
0.0000
传统热力熵增(热力)
lh15�15h
0.0000
ESes12��2es1
0.0000
传统热力熵增(热力)
lh16�16h
0.0060
ESes13��3es1
0.0000
传统热力熵增(ES1)
lES11�1ES1
0.0000
ESes14��4es1
0.0000
传统热力熵增(ES1)
lES12�2ES1
0.0000
ESes15��5es1
0.0000
传统热力熵增(ES1)
lES13�3ES1
0.0000
ESes21��1es2
0.0000
混合型熵增(ES1)
lES14�4ES1
0.9929
ESes22��2es2
0.0000
传统热力熵增(ES1)
lES21�1ES2
0.0000
ESes23��3es2
0.0000
传统热力熵增(ES1)
lES22�2ES2
0.0000
ESes24��4es2
0.0000
传统热力熵增(ES1)
lES23�3ES2
0.0000
ESes25��5es2
0.0000
混合型熵增(ES2)
lES24�4ES2
0.8036
“信息”熵增(电负荷)
E4�4
0.1412
“信息”熵增(气负荷)
G3�3
1.2954
“信息”熵增(气负荷)
G4�4
1.0100
“信息”熵增(气负荷)
G5�5
0.5046
“信息”熵增(热负荷)
Hh11�11h
0.0680
“信息”熵增(热负荷)
Hh12�12h
0.2039
“信息”熵增(热负荷)
Hh13�13h
0.1359
“信息”熵增(可再生能源)
E2�2
0.0299
“信息”熵增(可再生能源)
E3�3
0.0536
熵增总和
5.3118
5.3114
需要说明的是,表C1中电力、天然气及热力负荷引入了不确定性,对应的是信息学等效热力学熵增源,因此汇总在熵增源一列。
表C2节点(局部)熵态平衡关系验证比较(以联立求解为例)
TableC2Verificationandcomparisonofnodeentropystatebalancerelationship(simultaneoussolutionasexample)
系统节点
外部输入熵增流
网络输入熵增流
节点输入总熵增流
节点输出总熵增流
流向网络
熵增流
流向负荷
熵增流
E1�1
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
E2�2
0.0299
0.0001
0.0300
0.0300
0.0300
0.0000
E3�3
0.0536
0.5694
0.6230
0.6230
0.6230
0.0000
E4�4
0.0000
0.6235
0.6235
0.6235
0.0000
0.6235
E5�5
0.0000
0.0231
0.0231
0.0231
0.0000
0.0231
E6�6
0.5622
0.0000
0.5622
0.5622
0.5622
0.0000
G1�1
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
G2�2
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
G3�3
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
G4�4
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
G5�5
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
G6�6
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
G7�7
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
Hh1�1h
0.4306
0.0000
0.4306
0.4306
0.4306
0.0000
Hh2�2h
0.8267
0.0000
0.8267
0.8267
0.8267
0.0000
Hh3�3h
0.0000
0.2721
0.2721
0.2721
0.2721
0.0000
Hh4�4h
0.0000
0.4282
0.4282
0.4282
0.4282
0.0000
Hh5�5h
0.0000
0.8327
0.8327
0.8327
0.8327
0.0000
Hh6�6h
0.0000
0.1500
0.1500
0.1500
0.0000
0.1500
Hh7�7h
0.0000
0.1834
0.1834
0.1834
0.0000
0.1834
Hh8�8h
0.0000
0.0796
0.0796
0.0796
0.0796
0.0000
Hh9�9h
0.0000
0.1026
0.1026
0.1026
0.1026
0.0000
Hh10�10h
0.0000
0.1822
0.1822
0.1822
0.1822
0.0000
Hh11�11h
0.0000
0.2721
0.2721
0.2721
0.0796
0.1925
Hh12�12h
0.0000
0.4282
0.4282
0.4282
0.1026
0.3255
Hh13�13h
0.0000
0.6153
0.6153
0.6153
0.1378
0.4775
ESes11��1es1
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
ESes12��2es1
0.0000
0.5622
0.5622
0.5622
0.0000
0.5622
ESes13��3es1
0.0000
0.4306
0.4306
0.4306
0.0000
0.4306
ESes14��4es1
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
ESes15��5es1
0.0000
0.9929
0.9929
0.9929
0.9929
0.0000
ESes21��1es2
0.0231
0.0000
0.0231
0.0231
0.0231
0.0000
ESes22��2es2
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
ESes23��3es2
0.0000
0.8267
0.8267
0.8267
0.0000
0.8267
ESes24��4es2
0.0000
0.0231
0.0231
0.0231
0.0231
0.0000
ESes25��5es2
0.0000
0.8267
0.8267
0.8267
0.8267
0.0000
其中节点熵增为输入该节点的全部熵增流总和,包括由(外部)节点注入熵增流和(内部)网络支路输入该节点的熵增流,节点输出熵增为由该节点输出的全部熵增流,包括流向(内部)网络支路的熵增流和流向(外部)负荷节点的熵增流。
附录D由IES熵态机理模型可知:系统节点熵增流输出遵循(局部)节点熵态分配关系。为检验该关系,需要定义相应的分析变量。对于IES熵态网络中的各节点而言,称首端节点为该节点的支路为该节点的关联支路。定义节点关联支路㶲流比例系数αexergy,pr�exergy,pr,为该节点关联支路㶲流eb�b与该节点流出总㶲流eoN�oN之比,计算方法如下所示:
αexergy,pr=ebeoN�exergy,pr=�b�oN
(D1)
定义节点关联支路熵增流比例系数αentropy,pr�entropy,pr为该节点关联支路熵增流ΔSbΔ�b与该节点流出总熵增流ΔSoNΔ�oN之比,计算方法如下所示:
αentropy,pr=ΔSbΔSoN�entropy,pr=Δ�bΔ�oN
(D2)
当节点输出的总熵增流非零时,关联支路的αexergy,pr�exergy,pr与αentropy,pr�entropy,pr应当是一致的;对于节点输出总熵增流为零的节点,根据㶲流比例计算得出的关联支路熵增流也为零。经检验,所有支路均满足上述关系。具体统计与分析数据如表D1所示。
表D1节点熵态分配关系验证比较(以联立求解为例)
TableD1Verificationandcomparisonofnodeentropystatedistributionrelationship(simultaneoussolutionasexample)
节点
节点流出
总㶲流eoN�oN
节点流出
总熵增流ΔSoNΔ�oN
关联支路/
负荷
关联支路
㶲流eb�b
关联支路㶲流
比例系数αexergy,pr�exergy,pr
关联支路
熵增流ΔSbΔ�b
关联支路熵增流
比例系数αentropy,pr�entropy,pr
比例差值
E2�2
206.47
0.0300
le2�2e
48.55
23.51%
0.0071
23.51%
0.00%
le4�4e
157.93
76.49%
0.0229
76.49%
0.00%
G2�2
3682.73
0.0000
lg2�2g
1318.42
35.80%
0.0000
--
--
lg3�3g
1210.69
32.87%
0.0000
--
--
lg4�4g
1153.63
31.33%
0.0000
--
--
G3�3
1783.43
0.0000
lg7�7g
451.78
25.33%
0.0000
--
--
gL1
1331.66
74.67%
0.0000
--
--
G4�4
1530.34
0.0000
lg5�5g
465.01
30.39%
0.0000
--
--
gL2
1065.33
69.61%
0.0000
--
--
G5�5
1153.63
0.0000
lg6�6g
319.66
27.71%
0.0000
--
--
lg8�8g
123.75
10.73%
0.0000
--
--
gL3
710.22
61.56%
0.0000
--
--
Hh1�1h
93.20
0.4306
lh1�1h
20.37
21.86%
0.0941
21.85%
0.00%
lh2�2h
72.83
78.15%
0.3365
78.15%
0.00%
Hh5�5h
64.12
0.8327
lh3�3h
5.18
8.08%
0.0673
8.08%
0.00%
lh4�4h
11.56
18.03%
0.1501
18.03%
0.00%
lh13�13h
47.38
73.89%
0.6153
73.89%
0.00%
Hh8�8h
7.03
0.0796
lh6�6h
4.44
63.15%
0.0503
63.18%
0.04%
lh9�9h
2.59
36.84%
0.0293
36.82%
-0.02%
Hh9�9h
17.05
0.1026
lh7�7h
15.89
93.22%
0.0957
93.19%
-0.03%
lh8�8h
1.16
6.81%
0.0070
6.81%
0.00%
Hh11�11h
24.04
0.2721
lh14�14h
7.03
29.24%
0.0796
29.24%
0.01%
hL1
17.01
70.74%
0.1925
70.76%
0.02%
Hh12�12h
71.11
0.4282
lh15�15h
17.05
23.98%
0.1026
23.97%
-0.01%
hL2
54.06
76.02%
0.3255
76.03%
0.01%
Hh13�13h
47.38
0.6153
lh16�16h
10.61
22.39%
0.1378
22.40%
0.00%
hL3
36.77
77.60%
0.4775
77.60%
0.00%
ESes15��5es1
170.65
0.9929
lES12�2ES1
96.63
56.62%
0.5622
56.63%
0.00%
lES13�3ES1
74.02
43.38%
0.4306
43.37%
0.00%
E1�1
156.49
0.0000
le1�1e
156.49
100.00%
0.0000
--
--
E3�3
220.14
0.6230
le3�3e
220.14
100.00%
0.6230
100.00%
0.00%
E4�4
220.00
0.6235
eL1
220.00
100.00%
0.6235
100.00%
0.00%
E5�5
157.89
0.0231
ES2
157.89
100.00%
0.0231
100.00%
0.00%
E6�6
96.63
0.5622
le5�5e
96.63
100.00%
0.5622
100.00%
0.00%
G1�1
3682.73
0.0000
lg1�1g
3682.73
100.00%
0.0000
--
--
G6�6
451.78
0.0000
ES1
451.78
100.00%
0.0000
--
--
G7�7
123.75
0.0000
ES2
123.75
100.00%
0.0000
--
--
Hh2�2h
65.84
0.8267
lh5�5h
65.84
100.00%
0.8267
100.00%
0.00%
Hh3�3h
24.04
0.2721
lh11�11h
24.04
99.98%
0.2721
100.00%
0.02%
Hh4�4h
71.11
0.4282
lh12�12h
71.11
100.00%
0.4282
100.00%
0.00%
Hh6�6h
19.18
0.1500
ES1
19.18
100.00%
0.1500
100.00%
0.00%
Hh7�7h
11.73
0.1834
ES2
11.73
99.96%
0.1834
100.00%
0.04%
Hh10�10h
12.06
0.1822
lh10�10h
12.06
99.96%
0.1822
100.00%
0.04%
ESes11��1es1
451.78
0.0000
lES11�1ES1
451.78
100.00%
0.0000
--
--
ESes12��2es1
96.63
0.5622
H1
96.63
100.00%
0.5622
100.00%
0.00%
ESes13��3es1
74.02
0.4306
E6
74.02
100.01%
0.4306
100.00%
-0.01%
ESes14��4es1
451.78
0.0000
lES14�4ES1
451.78
100.00%
0.0000
--
--
ESes21��1es2
157.89
0.0231
lES21�1ES2
157.89
100.00%
0.0231
100.00%
0.00%
ESes22��2es2
123.75
0.0000
lES22�2ES2
123.75
100.00%
0.0000
--
--
ESes23��3es2
54.10
0.8267
H2
54.10
99.99%
0.8267
100.00%
0.01%
ESes24��4es2
281.65
0.0231
lES24�4ES2
281.65
100.00%
0.0231
100.00%
0.00%
ESes25��5es2
54.10
0.8267
lES23�3ES2
54.10
99.99%
0.8267
100.00%
0.01%
参考文献1
刘华军,石印,郭立祥,等.新时代的中国能源革命:历程、成就与展望[J].管理世界,2022,38(7):6-24.[百度学术]
LIUHuajun,SHIYin,GUOLixiang,’senergyreforminthenewera:process,achievementsandprospects[J].JournalofManagementWorld,2022,38(7):6-24.[百度学术]
2
张沈习,王丹阳,程浩忠,等.双碳目标下低碳综合能源系统规划关键技术及挑战[J].电力系统自动化,2022,46(8):189-207.[百度学术]
ZHANGShenxi,WANGDanyang,CHENGHaozhong,lanningforcarbonemissionpeakandcarbonneutrality[J].AutomationofElectricPowerSystems,2022,46(8):189-207.[百度学术]
3
胡枭,尚策,陈东文,等.考虑能量品质的区域综合能源系统多目标规划方法[J].电力系统自动化,2019,43(19):22-31.[百度学术]
HUXiao,SHANGCe,CHENDongwen,consideringenergyquality[J].AutomationofElectricPowerSystems,2019,43(19):22-31.[百度学术]
4
贾宏杰,穆云飞,余晓丹.对我国综合能源系统发展的思考[J].电力建设,2015,36(1):16-25.[百度学术]
JIAHongjie,MUYunfei,[J].ElectricPowerConstruction,2015,36(1):16-25.[百度学术]
5
王丹,周天烁,李家熙,等.面向能源转型的高㶲综合能源系统理论与应用[J].电力系统自动化,2022,46(17):114-131.[百度学术]
WANGDan,ZHOUTianshuo,LIJiaxi,ytransition[J].AutomationofElectricPowerSystems,2022,46(17):114-131.[百度学术]
6
KHOSHGOFTARMANESHMH,MOUSAVIRABETISA,NOURPOURM,,exergy,exergoeconomic,andexergoenvironmentalanalysisofaninnovativesolar-geothermal-gasdrivenpolygenerationsystemforcombinedpower,hydrogen,hotwater,andfreshwaterproduction[J].SustainableEnergyTechnologiesandAssessments,2022,51:101861.[百度学术]
7
李家熙,王丹,贾宏杰,等.面向可再生能源接入的综合能源系统熵态机理和分析方法[J].电力系统自动化,2023,47(9):47-58.[百度学术]
LIJiaxi,WANGDan,JIAHongjie,orintegrationofrenewableenergy[J].AutomationofElectricPowerSystems,2023,47(9):47-58.[百度学术]
8
李家熙,王丹,周天烁,等.面向综合能源系统的㶲流计算模型[J].电力系统自动化,2022,46(24):45-56.[百度学术]
LIJiaxi,WANGDan,ZHOUTianshuo,[J].AutomationofElectricPowerSystems,2022,46(24):45-56.[百度学术]
9
陈忠华,高振宇,陈嘉敏,等.考虑不确定性因素的综合能源系统协同规划研究[J].电力系统保护与控制,2021,49(8):32-40.[百度学术]
CHENZhonghua,GAOZhenyu,CHENJiamin,inguncertainty[J].PowerSystemProtectionandControl,2021,49(8):32-40.[百度学术]
10
黎静华,黄玉金,张鹏.综合能源系统多能流潮流计算模型与方法综述[J].电力建设,2018,39(3):1-11.[百度学术]
LIJinghua,HUANGYujin,ergysystem[J].ElectricPowerConstruction,2018,39(3):1-11.[百度学术]
11
LIJX,WANGD,JIAHJ,tioninregionalintegratedenergysystem[J].AppliedEnergy,2022,324:119725.[百度学术]
12
WANGY,ZHANGN,KANGCQ,[J].IEEETransactionsonSmartGrid,2019,10(1):257-270.[百度学术]
13
刘芸江,胡海涛,杨孝伟,等.24kV柔性直流牵引供电系统潮流计算方法与供电特性分析[J].电工技术学报,2023,38(9):2323-2334.[百度学术]
LIUYunjiang,HUHaitao,YANGXiaowei,alysisof24kVflexibledirectcurrenttractionpowersystem[J].TransactionsofChinaElectrotechnicalSociety,2023,38(9):2323-2334.[百度学术]
14
周天烁,王丹,李家熙,等.面向综合能源系统的㶲流追踪模型与计算方法[J].电力系统自动化,2023,47(17):75-88.[百度学术]
ZHOUTianshuo,WANGDan,LIJiaxi,system[J].AutomationofElectricPowerSystems,2023,47(17):75-88.[百度学术]
15
李家熙,王丹,贾宏杰.面向综合能源系统的㶲流机理与分析方法[J].电力系统自动化,2022,46(12):163-173.[百度学术]
LIJiaxi,WANGDan,[J].AutomationofElectricPowerSystems,2022,46(12):163-173.[百度学术]
16
LIJX,WANGD,JIAHJ,:anovelenergyhubmodelconsideringenergyquality[C]//IEEEPowerEnergySocietyGeneralMeeting(PESGM),July17-21,2022,Denver,USA.[百度学术]
17
张丹阳.区域综合能源系统多能源站运行优化方法研究[D].北京:华北电力大学,2022.[百度学术]
nalcomprehensiveenergysystem[D].Beijing:NorthChinaElectricPowerUniversity,2022.[百度学术]
18
李宜哲,王丹,贾宏杰,等.综合能源系统能量枢纽多样性建模和典型适用性研究[J].综合智慧能源,2023,45(7):22-29.[百度学术]
LIYizhe,WANGDan,JIAHongjie,theirtypicalapplications[J].IntegratedIntelligentEnergy,2023,45(7):22-29.[百度学术]
19
左丽丽,吴长春,丁明江.输配气管网稳态仿真问题的拓广[J].中国石油大学学报(自然科学版),2006,30(1):111-114.[百度学术]
ZUOLili,WUChangchun,[J].JournalofChinaUniversityofPetroleum(EditionofNaturalScience),2006,30(1):111-114.[百度学术]
20
MIAOCR,WANGQ,straints[J].ProtectionandControlofModernPowerSystems,2023,8(1):18.[百度学术]
21
ZHUMT,XUCS,DONGSF,-thermalintegratedenergysystems[J].ProtectionandControlofModernPowerSystems,2021,6(1):5.[百度学术]
22
邓红雷,张莉彬,唐崇旺,等.一种含分布式电源的配电网三相潮流混合计算方法[J].电力系统保护与控制,2020,48(14):10-17.[百度学术]
DENGHonglei,ZHANGLibin,TANGChongwang,nerationresourceonadistributionnetwork[J].PowerSystemProtectionandControl,2020,48(14):10-17.[百度学术]
23
LEIY,WANGD,JIAHJ,nalcorrelationscenariogenerationmethodforregionalintegratedenergysystemintegratedrenewableenergy[J].AppliedEnergy,2020,276:115395.[百度学术]
本文链接:https://goko.jsntrg.cn/514091761527.html
